题目内容
10.供电站对电价执行时段收费,全天分为平、谷两个时段,平段为8:00~22:00,14小时,谷段为22:00~次日8:00,10小时.平段用电价格在原销售电价基础上每千瓦时上浮0.03元,谷段电价在原销售电价基础上每千瓦时下浮0.25元.小明家2月份实用平段电量40千瓦时,谷段电量60千瓦时,按分时电价付费42.73元.(1)问小明该月支付的平段、谷段电价每千瓦时各为多少元?
(2)如不使用分时电价结算,2月份小明家将多支付电费多少元?
分析 (1)设原销售电价为每千瓦时x元,平段用电费用+谷段用电费用=42.73元,即:40(原售电价+0.03元)+60(原售电价-0.25元)=42.73元,据此列方程求解;
(2)求出原售电价,已知2月份的用电量,就比较容易求出:如不使用分时电价结算,2月份小明家将支付电费.从而算出多支付的电费数.
解答 解:(1)设原销售电价为每千瓦时x元,
根据题意得:40×(x+0.03)+60×(x-0.25)=42.73
解得:x=0.5653,
∴当x=0.5653时,x+0.03=0.5953,
x-0.25=0.3153.
答:小明家该月支付平段电价为每千瓦时0.5953元、谷段电价每千瓦时0.3153元;
(2)100×0.5653-42.73=13.8(元).
答:如不使用分时电价结算,小明家2月份将多支付13.8元.
点评 本题考查了一元一次方程的应用,解答本题的关键是读懂题意,设出未知数,正确找出题目中的相等关系,列方程求解.

练习册系列答案
相关题目
5.设α、β为方程2x2+4x-1=0的两个实数根,则α+β-1的值为( )
| A. | 3 | B. | -3 | C. | 1 | D. | .-1 |
15.|-sin60°|的相反数是( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
2.地球与太阳的距离约为150000000千米;将数字150000000用科学记数法表示为( )
| A. | 15×107千米 | B. | 1.5千米 | C. | 1.5×108千米 | D. | 0.15×107千米 |
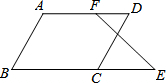 已知:如图,AB∥CD.∠A+∠DCE=180°,求证:∠E=∠DFE.
已知:如图,AB∥CD.∠A+∠DCE=180°,求证:∠E=∠DFE.