题目内容
2.x2+y=3,当-1≤x≤2时,y的最小值是-1.分析 先根据-1≤x≤2,求出1≤x2≤4,然后根据x2+y=3得出y=3-x2,将x2的最大值代入求解即可.
解答 解:∵x2+y=3,
∴y=3-x2,
∵-1≤x≤2,
∴1≤x2≤4,
∴当x2=4时,
y的最小值为:3-4=-1.
故答案为:-1.
点评 本题考查了二次函数的最值,解答本题的关键在于先根据-1≤x≤2,求出1≤x2≤4,然后根据x2+y=3得出y=3-x2,将x2的最大值代入求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知m+n=3,则m2+2mn+n2-6的值( )
| A. | 12 | B. | 6 | C. | 3 | D. | 0 |
 用-4、-3、-2、-1、0、1、2、3、4这9个数填在图中.使得横行、竖行、对角线之和为0.
用-4、-3、-2、-1、0、1、2、3、4这9个数填在图中.使得横行、竖行、对角线之和为0.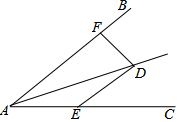 如图:∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=10,则DF等于5.
如图:∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=10,则DF等于5.