题目内容
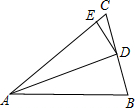
14.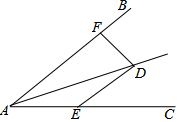 如图:∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=10,则DF等于5.
如图:∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=10,则DF等于5.
分析 过D作DM⊥AC,根据直角三角形的性质可得DM=$\frac{1}{2}$DE,再由DE∥AB可得∠BAD=∠ADE=15°,进而可得AD平分∠BAC,再根据角平分线的性质可得DF=DM,进而可得答案.
解答 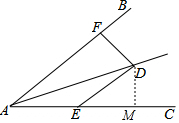 解:过D作DM⊥AC,
解:过D作DM⊥AC,
∵∠DAE=∠ADE=15°,
∴∠DEC=30°,AE=DE,
∵AE=10,
∴DE=10,
∴DM=5,
∵DE∥AB,
∴∠BAD=∠ADE=15°,
∴∠BAD=∠DAC,
∵DF⊥AB,DM⊥AC,
∴DF=DM=5.
故答案为:5.
点评 此题主要考查了角平分线的性质,关键是掌握直角三角形30°角所对的边等于斜边的一半,角的平分线上的点到角的两边的距离相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.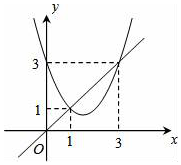 函数y=x2+bx+c与y=x的图象如图所示,有以下结论①b2-4c≥0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b-1)x+c<0.其中正确的个数为( )
函数y=x2+bx+c与y=x的图象如图所示,有以下结论①b2-4c≥0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b-1)x+c<0.其中正确的个数为( )
 函数y=x2+bx+c与y=x的图象如图所示,有以下结论①b2-4c≥0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b-1)x+c<0.其中正确的个数为( )
函数y=x2+bx+c与y=x的图象如图所示,有以下结论①b2-4c≥0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b-1)x+c<0.其中正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
4. 如图,在△ABC中,AB=AC,BD=CD,∠BAD=20°,DE⊥AC于E.则∠EDC的大小是( )
如图,在△ABC中,AB=AC,BD=CD,∠BAD=20°,DE⊥AC于E.则∠EDC的大小是( )
 如图,在△ABC中,AB=AC,BD=CD,∠BAD=20°,DE⊥AC于E.则∠EDC的大小是( )
如图,在△ABC中,AB=AC,BD=CD,∠BAD=20°,DE⊥AC于E.则∠EDC的大小是( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |