题目内容
6.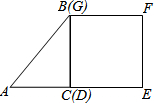 如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一条直线上,开始时点C与点D重合.将△ABC沿直线DE向右平移,直到点A与点E重合为止.设CD的长为x,若△ABC与正方形DEFG重合部分的面积为y,则y与x的函数图象是( )
如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一条直线上,开始时点C与点D重合.将△ABC沿直线DE向右平移,直到点A与点E重合为止.设CD的长为x,若△ABC与正方形DEFG重合部分的面积为y,则y与x的函数图象是( )| A. | 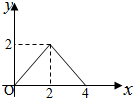 | B. | 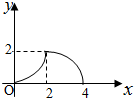 | C. | 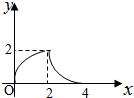 | D. | 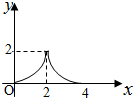 |
分析 按照x的取值范围分为当0≤x<2时,当2≤x<4时,分段根据重合部分的图形求面积,得出y是x的二次函数,即可得出结论.
解答 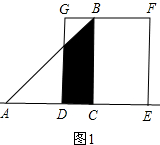 解:分两种情况:
解:分两种情况:
①如图1,
当0≤x<2时,y=$\frac{1}{2}$x(2+2-x)=-$\frac{1}{2}$x2+2x;
②如图2,
当2≤x≤4时,y=$\frac{1}{2}$(4-x)2;
故选:C.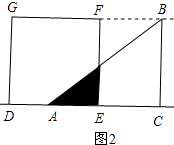
点评 本题考查了动点问题的函数图象、正方形及等腰直角三角形的性质.关键是根据图形的特点,分段求函数关系式.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
11.在?ABCD中,如果添加一个条件,就可推出?ABCD是矩形,那么添加的条件可以是( )
| A. | AB=BC | B. | AC=BD | C. | AC⊥BD | D. | AB⊥BD |
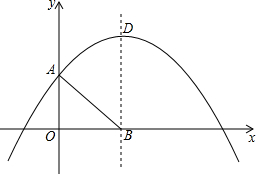 已知在直角坐标系中,抛物线y=ax2-8ax+3(a<0)与y轴交于点A,顶点为D,其对称轴交x轴于点B,点P在抛物线上,且位于抛物线对称轴的右侧.
已知在直角坐标系中,抛物线y=ax2-8ax+3(a<0)与y轴交于点A,顶点为D,其对称轴交x轴于点B,点P在抛物线上,且位于抛物线对称轴的右侧.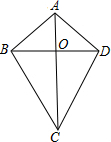 如图,四边形ABCD中,AB=AD,CB=CD,则称该四边形为“筝形”.连接对角线AC、BD,交于点O.
如图,四边形ABCD中,AB=AD,CB=CD,则称该四边形为“筝形”.连接对角线AC、BD,交于点O.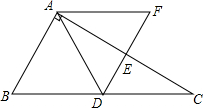 如图,Rt△ABC中,∠BAC=90°,∠C=30°.点D、E分别是边BC、AC的中点,DE的联线与BC的平行线AF交于点F.
如图,Rt△ABC中,∠BAC=90°,∠C=30°.点D、E分别是边BC、AC的中点,DE的联线与BC的平行线AF交于点F.