题目内容
1. 如图,在四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O,求证:EF与BD互相平分.
如图,在四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O,求证:EF与BD互相平分.
分析 根据平行四边形的判定与性质,可得AD与BC的位置关系,根据平行线的性质,可得∠OBE与∠ODF的关系,∠OEB与∠OFD的关系,根据等式的性质,可得AD与BE的关系,根据全等三角形的判定与性质,可得答案.
解答 证明:∵AB=DC,AD=BC,
∴四边形ABCD是平行四边形,
∴AD∥BC,
∴∠OBE=∠ODF,∠OEB=∠OFD.
∵AD=BC,AF=CE,
∴BE=FD.
在△OBE和△ODF中,
$\left\{\begin{array}{l}{∠OBE=∠ODF}\\{BE=DF}\\{∠OEB=∠OFD}\end{array}\right.$,
∴△OBE≌△ODF(ASA),
∴OB=OD,OE=OF,
即EF与BD互相平分.
点评 本题考查了平行四边形的判定与性质,利用了平行四边形的判定与性质,全等三角形的判定与性质.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
11.下面调查中,适宜采用全面调查方式的是( )
| A. | 调查全国中小学生身体素质状况 | |
| B. | 调查重庆市冷饮市场某种品牌冰淇淋的质量情况 | |
| C. | 调查我校初2013级某班学生出生日期 | |
| D. | 调查我国居民对汽车废气污染环境的看法 |
12.据媒体预测报道说,2015年中国GDP总和将达到687380亿美元,将其中的687380亿美元化成科学记数法( )
| A. | 68738×108 | B. | 687380×108 | C. | 6.8738×1013 | D. | 6.8738×1012 |
1. 如图,在边长为(a+2)的正方形中央剪去一边长为a的小正方形,则阴影部分的面积为( )
如图,在边长为(a+2)的正方形中央剪去一边长为a的小正方形,则阴影部分的面积为( )
 如图,在边长为(a+2)的正方形中央剪去一边长为a的小正方形,则阴影部分的面积为( )
如图,在边长为(a+2)的正方形中央剪去一边长为a的小正方形,则阴影部分的面积为( )| A. | 4 | B. | 4a | C. | 4a+4 | D. | 2a+4 |
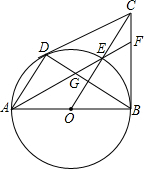 如图,已知AB为⊙O的直径,CD、CB为⊙O的切线,D、B为切点,OC交⊙O于点E,AE的延长线交BC于点F,连接AD、BD.给出以下结论:①AD∥OC;②FC=FE;③点E为△CDB的内心.其中正确的是①③(填序号).
如图,已知AB为⊙O的直径,CD、CB为⊙O的切线,D、B为切点,OC交⊙O于点E,AE的延长线交BC于点F,连接AD、BD.给出以下结论:①AD∥OC;②FC=FE;③点E为△CDB的内心.其中正确的是①③(填序号).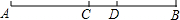 如图,点C是线段AB的中点.
如图,点C是线段AB的中点.