题目内容
12.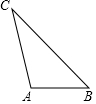 如图,△ABC是一块三角边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )
如图,△ABC是一块三角边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )| A. | 三条高的交点 | B. | 三条中线的交点 | ||
| C. | 三边垂直平分线的交点 | D. | 三个内角角平分线的交点 |
分析 根据题意得到圆形薄板的圆心应是△ABC的内心,根据内心的性质解答即可.
解答 解:要在△ABC薄板中裁剪出一个面积最大的圆形薄板,
则作△ABC的内切圆,即作△ABC的三个内角角平分线的交点,
故选:D.
点评 本题考查的是三角形的内切圆与内心,掌握三角形的内心就是三角形三个内角角平分线的交点是解题的关键.

练习册系列答案
相关题目
7.方程2x-y=0,5x+3xy=2,3x-y-2x=$\frac{1}{4}$,x2+2x-1=0,$\frac{3}{x}$-2y=5,3x=2y中,二元一次方程的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.若分式$\frac{|x|-3}{x-3}$的值为零,则x的值应取( )
| A. | x=3 | B. | x=-3 | C. | x=±3 | D. | x=0 |
4.龙华轻轨将于2017年6月底投入使用,拟在轨道沿途种植花木共20000棵,为尽量减少施工队交通所造成的影响,实际施工时每天的工效比原计划提高25%,结果提前5天完成种植任务,设原计划每天种植花木x棵,根据题意可列方程为( )
| A. | $\frac{2000}{x}$-$\frac{20000}{x(1-25%)}$=5 | B. | $\frac{20000}{x(1+25%)}$-$\frac{20000}{x}$=5 | ||
| C. | $\frac{20000}{x(1-25%)}$-$\frac{20000}{x}$=5 | D. | $\frac{20000}{x}$-$\frac{2000}{x(1+25%)}$=5 |
1.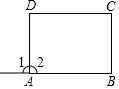 如图,已知∠1=∠B,∠2=∠C,则下列结论不成立的是( )
如图,已知∠1=∠B,∠2=∠C,则下列结论不成立的是( )
 如图,已知∠1=∠B,∠2=∠C,则下列结论不成立的是( )
如图,已知∠1=∠B,∠2=∠C,则下列结论不成立的是( )| A. | AD∥BC | B. | ∠B=∠C | C. | ∠2+∠B=180° | D. | AB∥CD |
2.下列各题中,适合用平方差公式计算的是( )
| A. | (3a+b)(3b-a) | B. | ($\frac{1}{3}a$+1)(-$\frac{1}{3}a$-1) | C. | (a-b)(-a+b) | D. | (-a-b)(-a+b) |
 如图,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴上,点B坐标为(4,t)(t>0),二次函数y=x2+bx(b<0)的图象经过点B,顶点为点D.
如图,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴上,点B坐标为(4,t)(t>0),二次函数y=x2+bx(b<0)的图象经过点B,顶点为点D.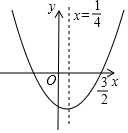 如图,已知二次函数y=ax2+bx+c的图象如图所示,则下列四个结论:①a+b+c<0;②a+c=b;③b=-2a;④4ac-b2<0,其中正确的结论有( )
如图,已知二次函数y=ax2+bx+c的图象如图所示,则下列四个结论:①a+b+c<0;②a+c=b;③b=-2a;④4ac-b2<0,其中正确的结论有( )