题目内容
11.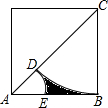 如图,正方形ABCD的边长为2,以CB为半径的弧交AC于D,以AD为半径的弧交AB于E,则图中阴影部分的面积为2-(2-$\sqrt{2}$)π.
如图,正方形ABCD的边长为2,以CB为半径的弧交AC于D,以AD为半径的弧交AB于E,则图中阴影部分的面积为2-(2-$\sqrt{2}$)π.
分析 阴影部分面积等于正方形面积的一半减去半径为2,圆心角为45°的扇形CDB和半径为2$\sqrt{2}$-2,圆心角为45°的扇形ADE,由此求得答案即可.
解答 解:∵正方形ABCD的边长为2,
∴AC=2$\sqrt{2}$,且∠DAE=∠BCD=45°,
∴阴影部分的面积为$\frac{1}{2}$×2×2-($\frac{45×π×{2}^{2}}{360}$+$\frac{45×π×(2\sqrt{2}-2)^{2}}{360}$)
=2-($\frac{π}{2}$+$\frac{(3-2\sqrt{2})π}{2}$)
=2-(2-$\sqrt{2}$)π.
故答案为:2-(2-$\sqrt{2}$)π.
点评 本题考查了扇形面积的计算,正方形的性质,把求阴影部分面积转化为基本平面图形面积的和与差是解决问题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
6.计算22+22+22+22的结果是( )
| A. | 23 | B. | 82 | C. | 24 | D. | 28 |
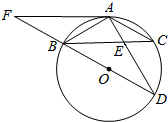 如图,BD为⊙O的直径,AB=AC,AD交BC于点E,延长DB交⊙O的切线AF于点F,AE=2,ED=4.
如图,BD为⊙O的直径,AB=AC,AD交BC于点E,延长DB交⊙O的切线AF于点F,AE=2,ED=4.
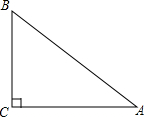 如图,△ABC中,∠C=90°.
如图,△ABC中,∠C=90°.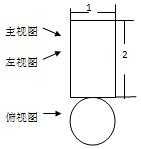 如图,长方形是一个几何体从正面看和从左面看到的形状图,圆是从上面看到的形状图(含有数据),则这个几何体的侧面展开图的面积等于( )
如图,长方形是一个几何体从正面看和从左面看到的形状图,圆是从上面看到的形状图(含有数据),则这个几何体的侧面展开图的面积等于( )