题目内容
7.根据给出的数轴及已知条件,解答下面的问题:
(1)已知点A,B,C表示的数分别为1,-$\frac{5}{2}$,-3观察数轴,与点A的距离为3的点表示的数是4或-2,B,C两点之间的距离为$\frac{1}{2}$;
(2)若将数轴折叠,使得A点与C点重合,则与B点重合的点表示的数是$\frac{1}{2}$;若此数轴上M,N两点之间的距离为2015(M在N的左侧),且当A点与C点重合时,M点与N点也恰好重合,则M,N两点表示的数分别是:M-1008.5,N1006.5;
(3)若数轴上P,Q两点间的距离为m(P在Q左侧),表示数n的点到P,Q两点的距离相等,则将数轴折叠,使得P点与Q点重合时,P,Q两点表示的数分别为:Pn-$\frac{m}{2}$,Qn+$\frac{m}{2}$(用含m,n的式子表示这两个数).
分析 (1)分点在A的左边和右边两种情况解答;利用两点之间的距离计算方法直接计算得出答案即可;
(2)A点与C点重合,得出对称点位-1,然后根据两点之间的距离列式计算即可得解;
(3)根据(2)的计算方法,然后分别列式计算即可得解.
解答 解:(1)点A的距离为3的点表示的数是1+3=4或1-3=-2;
B,C两点之间的距离为-$\frac{5}{2}$-(-3)=$\frac{1}{2}$;
(2)B点重合的点表示的数是:-1+[-1-(-$\frac{5}{2}$)]=$\frac{1}{2}$;
M=-1-$\frac{2015}{2}$=-1008.5,n=-1+$\frac{2015}{2}$=1006.5;
(3)P=n-$\frac{m}{2}$,Q=n+$\frac{m}{2}$.
故答案为:4或-2,$\frac{1}{2}$;$\frac{1}{2}$,-1008.5,1006.5;n-$\frac{m}{2}$,n+$\frac{m}{2}$.
点评 本题考查了数轴的运用.关键是利用数轴,数形结合求出答案,注意不要漏解.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目

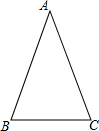 如图,在△ABC中,AB=AC.
如图,在△ABC中,AB=AC.