题目内容
2.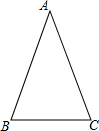 如图,在△ABC中,AB=AC.
如图,在△ABC中,AB=AC.(1)若∠A=α,求AB与BC的数量关系(用含α的式子表示);
(2)若∠B=α,求AB与BC的数量关系(用含α的式子表示).
分析 (1)过A点作AD⊥BC,根据等腰三角形的性质和三角形内角和定理可求∠B的度数,再根据等腰三角形的性质和三角函数即可求解;
(2)根据等腰三角形的性质和三角函数即可求解.
解答 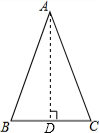 解:(1)过A点作AD⊥BC,
解:(1)过A点作AD⊥BC,
∵AB=AC,∠A=α,
∴∠B=90°-$\frac{1}{2}$α,
∴BD=AB•cos(90°-$\frac{1}{2}$α),
∴BC=2AB•cos(90°-$\frac{1}{2}$α);
(2)∵∠B=α,
∴BD=AB•cosα,
∴BC=2AB•cosα.
点评 考查了等腰三角形的性质:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.同时考查了三角形内角和定理和三角函数.

练习册系列答案
相关题目
 已知:如图,AB∥A′B′,BC∥B′C′,B′C′交AB于D,求证:∠B+∠B′=180°.
已知:如图,AB∥A′B′,BC∥B′C′,B′C′交AB于D,求证:∠B+∠B′=180°. 如图,∠ABC=120°,BF、BE分别是∠ABD、∠CBD的角平分线,则∠EBF的度数为60°.
如图,∠ABC=120°,BF、BE分别是∠ABD、∠CBD的角平分线,则∠EBF的度数为60°.