题目内容
16.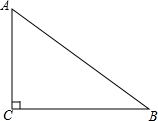 如图,Rt△ABC中,∠ACB=90°,AC=3,AB=5,若以点C为圆心,2.3为半径作⊙C,则直线AB与⊙C的位置关系是( )
如图,Rt△ABC中,∠ACB=90°,AC=3,AB=5,若以点C为圆心,2.3为半径作⊙C,则直线AB与⊙C的位置关系是( )| A. | 相离 | B. | 相切 | C. | 相交 | D. | 无法确定 |
分析 由勾股定理求出BC,根据题意可求得直角三角形斜边上的高,再根据直线和圆的位置关系,判断圆心到直线AB的距离与2的大小关系,从而确定⊙C与AB的位置关系.
解答 解:∵∠ACB=90°,AC=3,
∴BC=$\sqrt{{5}^{2}-{3}^{2}}$=4,
根据三角形的面积公式得:3×4=5×斜边上的高,
∴斜边上的高=$\frac{12}{5}$=2.4>2.3,
即d>r,
∴⊙C与AB相离.
故选:A.
点评 本题考查了直线和圆的位置关系;解题的根据是直线和圆相离?圆心到直线的距离大于圆的半径.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
11.方程3x2-2x-1=0的二次项系数和常数项分别为( )
| A. | 3和-2 | B. | 3和-1 | C. | 3和2 | D. | 3和1 |
6.在△ABC中,CO为AB边上的中线,且OC=$\frac{1}{2}$AB,以点O为圆心,OC长为半径画圆,延长CO交⊙O于点D,连结AD,BD,则四边形ADBC是( )
| A. | 正方形 | B. | 矩形 | ||
| C. | 菱形 | D. | 邻边相等的四边形 |
 如图中大、小正方形的边长分别为a和b,请用含a、b的代数式表示图中阴影部分的面积并化简.
如图中大、小正方形的边长分别为a和b,请用含a、b的代数式表示图中阴影部分的面积并化简. 如图,管中放置着三根同样的绳子AA1、BB1、CC1.小明在左侧选两个打一个结,小红在右侧选两个打一个结,则这三根绳子能连结成一根长绳的概率为$\frac{2}{3}$.
如图,管中放置着三根同样的绳子AA1、BB1、CC1.小明在左侧选两个打一个结,小红在右侧选两个打一个结,则这三根绳子能连结成一根长绳的概率为$\frac{2}{3}$.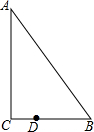 如图,Rt△ABC中,∠ACB=90°,∠B=50°,BC=3,且BD=2CD,将线段DB绕点D逆时针方向旋转至DB′,当点B′刚好旋转到△ABC的边上,且△DBB′为等腰三角形时旋转角的度数为80°或120°.
如图,Rt△ABC中,∠ACB=90°,∠B=50°,BC=3,且BD=2CD,将线段DB绕点D逆时针方向旋转至DB′,当点B′刚好旋转到△ABC的边上,且△DBB′为等腰三角形时旋转角的度数为80°或120°.