题目内容
8.已知数轴上的点A,B对应的数分别是x,y,且|x+100|+(y-200)2=0,点P为数轴上从原点出发的一个动点,速度为30单位长度/秒.(1)求点A,B两点之间的距离;
(2)若点A向右运动,速度为10单位长度/秒,点B向左运动,速度为20单位长度/秒,点A,B和P三点同时开始运动,点P先向右运动,遇到点B后立即掉后向左运动,遇到点A再立即掉头向右运动,如此往返,当A,B两点相距30个单位长度时,点P立即停止运动,求此时点P移动的路程为多少个单位长度?
(3)若点A,B,P三个点都向右运动,点A,B的速度分别为10单位长度/秒,20单位长度/秒,点M、N分别是AP、OB的中点,设运动的时间为t(0<t<10),在运动过程中①$\frac{OA-PB}{MN}$的值不变;②$\frac{OA+PB}{MN}$的值不变,可以证明,只有一个结论是正确的,请你找出正确的结论并求值.
分析 (1)根据非负数的性质求出x,y的值,利用两点间的距离公式即可求出点A,B两点之间的距离;
(2)设点P运动时间为x秒时,A,B两点相距30个单位长度.分A,B两点相遇前相距30个单位长度与A,B两点相遇后相距30个单位长度两种情况分别列出方程,解方程求出x的值,再根据路程=速度×时间即可求解;
(3)先求出运动t秒后A、P、B三点所表示的数为-100+10t,30t,200+20t,再利用利用中点的定义得出N表示的数为100+10t,M表示的数为20t-50,进而求解即可.
解答 解:(1)A、-100 B、200 AB=300
(2)设点P运动时间为x秒时,A,B两点相距30个单位长度.
由题意得10x+20x=300-30,10x+20x=300+30,
解得x=9,或x=11,
则此时点P移动的路程为30×9=270,或30×11=330.
答:P走的路程为270或330;
(3)运动t秒后A、P、B三点所表示的数为-100+10t,30t,200+20t,
∵0<t<10,
∴PB=200-10t,OA=100-10t,
PA=30t+100-10t=20t+100,OB=200+20t,
∵N为OB中点,M为AP中点,
∴N表示的数为100+10t,M表示的数为20t-50,
∴MN=150-10t,
∵OA+PB=300-20t,
∴$\frac{OA+PB}{MN}$=2,故②正确.
点评 本题考查了一元一次方程的应用,数轴,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
相关题目
16.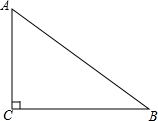 如图,Rt△ABC中,∠ACB=90°,AC=3,AB=5,若以点C为圆心,2.3为半径作⊙C,则直线AB与⊙C的位置关系是( )
如图,Rt△ABC中,∠ACB=90°,AC=3,AB=5,若以点C为圆心,2.3为半径作⊙C,则直线AB与⊙C的位置关系是( )
 如图,Rt△ABC中,∠ACB=90°,AC=3,AB=5,若以点C为圆心,2.3为半径作⊙C,则直线AB与⊙C的位置关系是( )
如图,Rt△ABC中,∠ACB=90°,AC=3,AB=5,若以点C为圆心,2.3为半径作⊙C,则直线AB与⊙C的位置关系是( )| A. | 相离 | B. | 相切 | C. | 相交 | D. | 无法确定 |
18.下面几个有理数最大的是( )
| A. | 2 | B. | 0 | C. | -3 | D. | -1 |
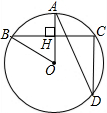 如图,在⊙O中,半径OA⊥弦BC于点H,点D在优弧BC上
如图,在⊙O中,半径OA⊥弦BC于点H,点D在优弧BC上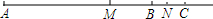 如图AB=48,C为线段AB的延长线上一点,M,N分别是AC,BC的中点.
如图AB=48,C为线段AB的延长线上一点,M,N分别是AC,BC的中点. 若要使图中平面展开图按虚线折叠成正方体后,相对面上两个数之和为6,则x+y=8.
若要使图中平面展开图按虚线折叠成正方体后,相对面上两个数之和为6,则x+y=8. 匀速地向一个容器内注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律大致如图所示(图中OABC为一折线),则这个容器的形状是( )
匀速地向一个容器内注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律大致如图所示(图中OABC为一折线),则这个容器的形状是( )