题目内容
8.某学校为九年级数学竞赛获奖选手购买以下三种奖品,其中小笔记本每本5元,大笔记本每本7元,钢笔每支10元,购买的大笔记本的数量是钢笔数量的2倍,共花费346元,若使购买的奖品总数最多,则这三种奖品的购买数量各为多少?分析 根据题意结合奖品的价格得出5x+7y+10z=346,y=2z,再利用共花费346元,分别得出x,y,z的取值范围,进而得出z的取值范围,分别分析得出所有的可能.
解答 解:设购买小笔记本x本,大笔记本y本,钢笔z支,
则有5x+7y+10z=346,y=2z,
易知0<x≤69,0<y≤49,0<z≤34,
∴5x+14z+10z=346,5x+24z=346,即x=$\frac{346-24z}{5}$.
∵x,y,z均为正整数,346-24z≥0,即0<z≤14,
∴z只能取14,9和4,
①当z为14时,x=$\frac{346-24z}{5}$=2,y=2z=28,x+y+z=44.
②当z为9时,x=$\frac{346-24z}{5}$=26,y=2z=18.x+y+z=53.
③当z为4时,x=$\frac{346-24z}{5}$=50,y=2z=8.x+y+z=62.
综上所述,若使购买的奖品总数最多,应购买小笔记本50本,大笔记本8本,钢笔4支.
点评 此题主要考查了三元一次不定方程,根据题意得出x,y,z的取值范围是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.有一个数阵排列如图:则第20行从左至右第10个数为( )


| A. | 425 | B. | 426 | C. | 427 | D. | 428 |
 有理数a,b如图所示,用“<”连接-a,|b|,a,b,0为b<-a<0<a<|b|.
有理数a,b如图所示,用“<”连接-a,|b|,a,b,0为b<-a<0<a<|b|.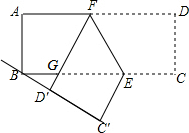 如图,矩形ABCD中,AB=4,AD=9,点E、F分别是BC、AD上的动点,∠FEC为钝角,沿直线EF翻折矩形,点C、D的对应点分别为C′、D′,若C′、D′、B在同一条直线上,且$\frac{BD′}{BC′}$=$\frac{1}{3}$时,则AF的长为3$\frac{5}{6}$.
如图,矩形ABCD中,AB=4,AD=9,点E、F分别是BC、AD上的动点,∠FEC为钝角,沿直线EF翻折矩形,点C、D的对应点分别为C′、D′,若C′、D′、B在同一条直线上,且$\frac{BD′}{BC′}$=$\frac{1}{3}$时,则AF的长为3$\frac{5}{6}$.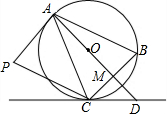 如图,AP是⊙O的切线,A为切点,AB是⊙O的弦,过点B作BC∥AP,交⊙O于点C,连接AC,过点C作CP∥AP于点P,连接AO并延长,交BC于点M,交过点C的直线于点D,且∠ACP=∠BCD
如图,AP是⊙O的切线,A为切点,AB是⊙O的弦,过点B作BC∥AP,交⊙O于点C,连接AC,过点C作CP∥AP于点P,连接AO并延长,交BC于点M,交过点C的直线于点D,且∠ACP=∠BCD