题目内容
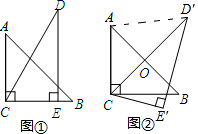 一副三角板如图①放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°斜边AB=4,CD=5.把三角板DCE绕着点C顺时针旋转15°得到△D′CE′(如图②),此时AB与CD′交于点O,则cos∠OAD′=
一副三角板如图①放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°斜边AB=4,CD=5.把三角板DCE绕着点C顺时针旋转15°得到△D′CE′(如图②),此时AB与CD′交于点O,则cos∠OAD′=考点:旋转的性质
专题:
分析:由∠ACB=∠DEC=90°,∠A=45°,∠D=30°,把三角板DCE绕着点C顺时针旋转15°得到△D′CE′,易求得∠ACD′的度数,又由三角形外角的性质,求得∠AOD′的度数,然后由等腰三角形的性质,求得OA=OB=OC=2,继而求得OD′=3,然后由勾股定理求得AD′的长,继而求得答案.
解答:解:如图②,根据题意得:∠BCE′=15°,
∵∠D′CE′=60°,
∴∠D′EB=45°,
∴∠ACD′=90°-45°=45°,
∴∠AOD′=∠CAB+∠ACD′=90°,
∵AC=BC,AB=4,
∴OA=OB=2,
∵∠ACB=90°,
∴CO=
AB=
×4=2,
又∵CD′=5,
∴OD′=CD′-OC=5-2=3,
∴AD′=
=
,
∴cos∠OAD′=
=
.
故答案为:
.
∵∠D′CE′=60°,
∴∠D′EB=45°,
∴∠ACD′=90°-45°=45°,
∴∠AOD′=∠CAB+∠ACD′=90°,
∵AC=BC,AB=4,
∴OA=OB=2,
∵∠ACB=90°,
∴CO=
| 1 |
| 2 |
| 1 |
| 2 |
又∵CD′=5,
∴OD′=CD′-OC=5-2=3,
∴AD′=
| OA2+OD′2 |
| 13 |
∴cos∠OAD′=
| OA |
| AD′ |
2
| ||
| 13 |
故答案为:
2
| ||
| 13 |
点评:此题考查了旋转的性质、等腰直角三角形的性质以及勾股定理.此题难度适中,注意掌握旋转前后图形的对应关系,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
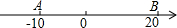 如图A、B两点在数轴上分别表示-10和20,动点P从点A出发以10个单位每秒的速度向右运动,动点Q从点B出发以每秒5个单位的速度出向右运动.设运动时间为t.
如图A、B两点在数轴上分别表示-10和20,动点P从点A出发以10个单位每秒的速度向右运动,动点Q从点B出发以每秒5个单位的速度出向右运动.设运动时间为t.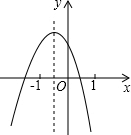 已知抛物线y=ax2+bx+c如图,则abc
已知抛物线y=ax2+bx+c如图,则abc 如图,已知∠A=∠E,∠C=∠D,EC=AD,求证:∠1=∠2.
如图,已知∠A=∠E,∠C=∠D,EC=AD,求证:∠1=∠2.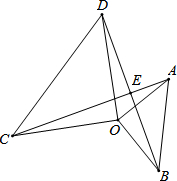 如图,等腰直角△AOB与等腰直角△COD有公共顶点O,点C、O、B不在同一条直线上,求证:
如图,等腰直角△AOB与等腰直角△COD有公共顶点O,点C、O、B不在同一条直线上,求证: 如图,在每个小正方形的边长均为1个单位长度的方格纸中,△ABO的顶点均与小正方形的顶点重合.以点O为坐标原点建立平面直角坐标系后,点A的坐标为(-2,4).
如图,在每个小正方形的边长均为1个单位长度的方格纸中,△ABO的顶点均与小正方形的顶点重合.以点O为坐标原点建立平面直角坐标系后,点A的坐标为(-2,4).