题目内容
如图，已知∠CAB=∠DBA 要使△ABC≌△BAD，只要增加的一个条件是考点：全等三角形的判定
专题：开放型
分析：由∠CAB=∠DBA，且AB=BA，可知需要再加一组对应边相等，或加一组对应角相等，可得出答案．
解答：解：
∵∠CAB=∠DBA，且AB=BA，
∴可再加条件：AC=BD，
在△ABC和△BAD中
∴△ABC≌△BAD（SAS），
故答案为：AC=BD（答案不唯一）．
∵∠CAB=∠DBA，且AB=BA，
∴可再加条件：AC=BD，
在△ABC和△BAD中
|
∴△ABC≌△BAD（SAS），
故答案为：AC=BD（答案不唯一）．
点评：本题主要考查全等三角形的判定，掌握全等三角形的判定方法是解题的关键，注意AAA和SAA是不能判定两个三角形全等的．
练习册系列答案
相关题目
如图，已知∠A=∠E，∠C=∠D，EC=AD，求证：∠1=∠2．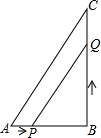
如图，△ABC中，∠B=90°，AB=6，BC=8，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动，当Q运动到C点时停止运动，P点也随之停止运动，如果点P、Q分别从点A、B同时出发．
如图，在每个小正方形的边长均为1个单位长度的方格纸中，△ABO的顶点均与小正方形的顶点重合．以点O为坐标原点建立平面直角坐标系后，点A的坐标为（-2，4）．
如图，在△ABC中，∠ACB=90°，CD是AB边上的高，∠A=30°，则（ ）A、AC=
| ||
B、CD=
| ||
C、BD=
| ||
D、AD=
|
已知一等腰三角形的腰长为3，底边长为2，底角为α．满足下列条件的三角形不一定与已知三角形全等的是（ ）
| A、两条边长分别为2，3，它们的夹角为α |
| B、两个角是α，它们的夹边为2 |
| C、三条边长分别是2，3，3 |
| D、两条边长是3，一个角是α |