题目内容
已知:AD,BE,CF是△ABC的中线,且交于点G.求证:AG:GD=BG:GE=CG:GF=2.
(这道题目是根据相似三角形的知识证明三角形重心的性质)
(这道题目是根据相似三角形的知识证明三角形重心的性质)
考点:三角形的重心,相似三角形的判定与性质
专题:证明题
分析:首先根据题意画出图形,连接EF,由三角形中位线的性质,可得EF∥BC,EF=
BC,继而可证得△EFG∽△BCG,然后由相似三角形的对应边成比例,证得GB:GE=GC:GF=2,同理可得AG:GD=BG:GE=2.
| 1 |
| 2 |
解答: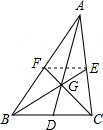 证明:如图,连接EF,
证明:如图,连接EF,
∵BE,CF分别是△ABC的中线,
∴EF∥BC,EF=
BC,
∴△EFG∽△BCG,
∴GB:GE=GC:GF=BC:EF=2.
同理,连接DE,可得AG:GD=BG:GE=2,
∴AG:GD=BG:GE=CG:GF=2.
 证明:如图,连接EF,
证明:如图,连接EF,∵BE,CF分别是△ABC的中线,
∴EF∥BC,EF=
| 1 |
| 2 |
∴△EFG∽△BCG,
∴GB:GE=GC:GF=BC:EF=2.
同理,连接DE,可得AG:GD=BG:GE=2,
∴AG:GD=BG:GE=CG:GF=2.
点评:此题考查了相似三角形的判定与性质以及三角形中位线的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
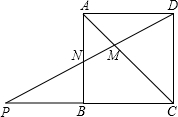 如图,正方形ABCD中,点N为AB的中点,连接DN并延长交CB的延长线于点P,连接AC交DN于点M.若PN=3,则DM的长为
如图,正方形ABCD中,点N为AB的中点,连接DN并延长交CB的延长线于点P,连接AC交DN于点M.若PN=3,则DM的长为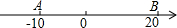 如图A、B两点在数轴上分别表示-10和20,动点P从点A出发以10个单位每秒的速度向右运动,动点Q从点B出发以每秒5个单位的速度出向右运动.设运动时间为t.
如图A、B两点在数轴上分别表示-10和20,动点P从点A出发以10个单位每秒的速度向右运动,动点Q从点B出发以每秒5个单位的速度出向右运动.设运动时间为t. 如图,已知∠A=∠E,∠C=∠D,EC=AD,求证:∠1=∠2.
如图,已知∠A=∠E,∠C=∠D,EC=AD,求证:∠1=∠2.