题目内容
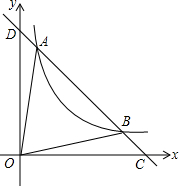 如图,已知直线y1=ax+b与反比例函数y2=
如图,已知直线y1=ax+b与反比例函数y2=| k |
| x |
(1)填空:a=
(2)当1≤x≤7时,请直接写出y2的取值范围是
(3)若y2=
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)先根据反比例函数y2=
(k>0)的图象过A(1,m)和B(6,1),可得k、m的值,代入一次函数的解析式可求得a、b的值.
(2)根据题意,结合图象,找A、C点,易得答案.
(3)根据A、B的坐标求得OA=OB,∠AOD=∠BOC,由S△AOP=S△BOP,则P到OA,OB的距离相等.P一定在∠AOB的平分线上,平分线的解析式是:y=x,代入反比例函数解析式即可求解.
| k |
| x |
(2)根据题意,结合图象,找A、C点,易得答案.
(3)根据A、B的坐标求得OA=OB,∠AOD=∠BOC,由S△AOP=S△BOP,则P到OA,OB的距离相等.P一定在∠AOB的平分线上,平分线的解析式是:y=x,代入反比例函数解析式即可求解.
解答:解:(1)根据题意,反比例函数y2=
(k>0)的图象交于A(1,m)和B(6,1),
易得k=6,m=6;
则y1=kx+b的图象也过点A(1,6),B(6,1);
代入解析式得
解得,a=-1,b=7;
故答案为-1,7,6.
(2)根据图象,当1≤x≤7时,0≤y≤6.
(3)∵A(1,6),B(6,1);
∴OA=OB,∠AOD=∠BOC,
∵S△AOP=S△BOP,
∴P到OA,OB的距离相等.
∴P一定在∠AOB的平分线上,
即在∠COD的平分线上,
∴平分线的解析式是:y=x.
把y=x代入y=
.
解得:x=y=
.
则P的坐标是:(
,
).
| k |
| x |
易得k=6,m=6;
则y1=kx+b的图象也过点A(1,6),B(6,1);
代入解析式得
|
解得,a=-1,b=7;
故答案为-1,7,6.
(2)根据图象,当1≤x≤7时,0≤y≤6.
(3)∵A(1,6),B(6,1);
∴OA=OB,∠AOD=∠BOC,
∵S△AOP=S△BOP,
∴P到OA,OB的距离相等.
∴P一定在∠AOB的平分线上,
即在∠COD的平分线上,
∴平分线的解析式是:y=x.
把y=x代入y=
| 6 |
| x |
解得:x=y=
| 6 |
则P的坐标是:(
| 6 |
| 6 |
点评:此题主要考查了反比例函数和一次函数的图象性质及待定系数法求解析式,要掌握它们的性质才能灵活解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在直角坐标系中,要将图形向左平移3个单位时,只需( )
| A、将图形上的每个点的横坐标减3,纵坐标不变 |
| B、将图形上的每个点的横坐标加3,纵坐标不变 |
| C、将图形上的每个点的横坐标不变,纵坐标减3 |
| D、将图形上的每个点的横坐标不变,纵坐标加3 |
 在Rt△ABC中,∠BAC=30°,斜边AB=2
在Rt△ABC中,∠BAC=30°,斜边AB=2 抛物线y=
抛物线y=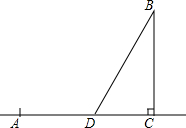 由沿河城市A运货物到离河岸30km的地点B,按沿河距离计算,B离A的沿河距离AC是40km.如果水路运费是公路运费的一半,应怎样确定在河岸上的D,从B修一条公路到D,使由A到B的运费最省?
由沿河城市A运货物到离河岸30km的地点B,按沿河距离计算,B离A的沿河距离AC是40km.如果水路运费是公路运费的一半,应怎样确定在河岸上的D,从B修一条公路到D,使由A到B的运费最省?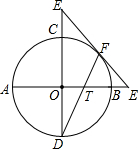 如图,AB和CD是互相垂直的两条直径,E为DC延长线上一点,EF切⊙O于点F,交AB的延长线于H,DF交AB于T,若tan∠D=
如图,AB和CD是互相垂直的两条直径,E为DC延长线上一点,EF切⊙O于点F,交AB的延长线于H,DF交AB于T,若tan∠D=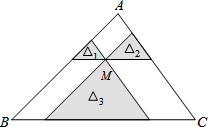 如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是
如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是