题目内容
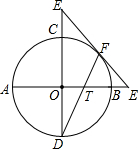 如图,AB和CD是互相垂直的两条直径,E为DC延长线上一点,EF切⊙O于点F,交AB的延长线于H,DF交AB于T,若tan∠D=
如图,AB和CD是互相垂直的两条直径,E为DC延长线上一点,EF切⊙O于点F,交AB的延长线于H,DF交AB于T,若tan∠D=| 1 |
| 3 |
考点:切线的性质
专题:计算题
分析:连结OF,如图,先在Rt△DOT中利用正切的定义得到tanD=
=
,则可设OT=x,OD=3x,再根据切线的性质得OF⊥EF,则∠OFH=90°,再证明∠HFD=∠HTF得到HF=HT,接着在Rt△OHF中利用勾股定理得到(3x)2+HF2=(x+HF)2,解得HF=4x,则OH=5x,于是根据正弦的定义得到sin∠HOF=
=
,然后根据等角的余角相等得到∠E=∠HOF,从而得到sin∠E=
.
| OT |
| OD |
| 1 |
| 3 |
| HF |
| OH |
| 4 |
| 5 |
| 4 |
| 5 |
解答: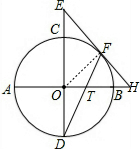 解:连结OF,如图,
解:连结OF,如图,
∵AB⊥CD,
∴∠DOB=90°,
在Rt△DOT中,∵tanD=
=
,
∴设OT=x,OD=3x,
∵EF切⊙O于点F,
∴OF⊥EF,
∴∠OFH=90°,
即∠OFD+∠DFH=90°,
∵∠D+∠DTO=90°,
而∠DTO=∠HTF,
∴∠D+∠HTF=90°,
∵OD=OF,
∴∠D=∠OFD,
∴∠HFD=∠HTF,
∴HF=HT,
在Rt△OHF中,OF=3x,OH=x+HT=x+HF,
∵OF2+HF2=OH2,
∴(3x)2+HF2=(x+HF)2,解得HF=4x,
∴OH=5x,
∴sin∠HOF=
=
=
,
∵∠E+∠EOF=90°,
∠HOF+∠EOF=90°,
∴∠E=∠HOF,
∴sin∠E=
.
 解:连结OF,如图,
解:连结OF,如图,∵AB⊥CD,
∴∠DOB=90°,
在Rt△DOT中,∵tanD=
| OT |
| OD |
| 1 |
| 3 |
∴设OT=x,OD=3x,
∵EF切⊙O于点F,
∴OF⊥EF,
∴∠OFH=90°,
即∠OFD+∠DFH=90°,
∵∠D+∠DTO=90°,
而∠DTO=∠HTF,
∴∠D+∠HTF=90°,
∵OD=OF,
∴∠D=∠OFD,
∴∠HFD=∠HTF,
∴HF=HT,
在Rt△OHF中,OF=3x,OH=x+HT=x+HF,
∵OF2+HF2=OH2,
∴(3x)2+HF2=(x+HF)2,解得HF=4x,
∴OH=5x,
∴sin∠HOF=
| HF |
| OH |
| 4x |
| 5x |
| 4 |
| 5 |
∵∠E+∠EOF=90°,
∠HOF+∠EOF=90°,
∴∠E=∠HOF,
∴sin∠E=
| 4 |
| 5 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了等腰三角形的判定和勾股定理.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
如图,点D是线段AB的中点,C是线段AD的中点,若AB=8cm,线段CD的长度为( )

| A、2cm | B、4cm |
| C、5cm | D、6cm |
 如图,平行四边形ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2且AC:BD=2:3,求平行四边形ABCD的面积.
如图,平行四边形ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2且AC:BD=2:3,求平行四边形ABCD的面积.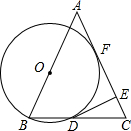 如图,⊙O的半径为3,⊙O切AC于F,交BC于D,DE⊥AC于E,CE=1,AB=AC,则AO=
如图,⊙O的半径为3,⊙O切AC于F,交BC于D,DE⊥AC于E,CE=1,AB=AC,则AO=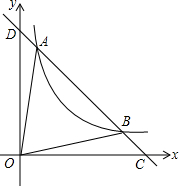 如图,已知直线y1=ax+b与反比例函数y2=
如图,已知直线y1=ax+b与反比例函数y2= 请在方格纸上画出与AB、CD垂直的线段,并用字母表示.
请在方格纸上画出与AB、CD垂直的线段,并用字母表示.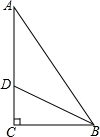 如图,BD平分∠ABC,a=4,BD=
如图,BD平分∠ABC,a=4,BD=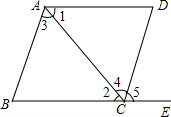 如图所示,在图中:
如图所示,在图中: