题目内容
10.在△ABC中,若2∠A=∠B=∠C,则△ABC是( )| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 无法确定 |
分析 运用三角形的内角和定理求出∠A=36°,进而求出∠B=∠C=72°,即可解决问题.
解答 解:在△ABC中,
∵2∠A=∠B=∠C,且∠A+∠B+∠C=180°,
∴5∠A=180°,∠A=36°,
∴∠B=∠C=72°,
∴△ABC是锐角等腰三角形.
故选B.
点评 本题主要考查了等腰三角形的定义、三角形的内角和定理及其应用问题;灵活运用三角形的内角和定理来解题是关键.

练习册系列答案
相关题目
18.下列说法正确的是( )
| A. | 同位角相等 | B. | 对顶角相等 | ||
| C. | 相等的角一定是对顶角 | D. | 角的大小与边的长短有关 |
5.如果点P在直线y=x+1上,则点P的坐标可以是( )
| A. | (1,1) | B. | (1,0) | C. | (2,0) | D. | (1,2) |
2.下列一元二次方程是一般形式的为( )
| A. | (x-1)2=0 | B. | 3x2-4x+1=0 | C. | x(x+5)=0 | D. | (x+6)2-9=0 |
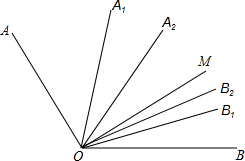 如图∠AOB=α°,OA1、OB1分别是∠AOM和∠MOB的平分线,OA2、OB2分别是∠A1OM和∠MOB1的平分线,OA3、OB3分别是∠A2OM和∠MOB2的平分线…OAn、OBn分别是∠An-1OM和∠MOBn-1的平分线,则∠AnOBn=$\frac{1}{{2}^{n}}$α°.
如图∠AOB=α°,OA1、OB1分别是∠AOM和∠MOB的平分线,OA2、OB2分别是∠A1OM和∠MOB1的平分线,OA3、OB3分别是∠A2OM和∠MOB2的平分线…OAn、OBn分别是∠An-1OM和∠MOBn-1的平分线,则∠AnOBn=$\frac{1}{{2}^{n}}$α°. 如图,一个小正方形网格的边长表示50米.A同学上学时从家中出发,先向东走250米,再向北走50米就到达学校.
如图,一个小正方形网格的边长表示50米.A同学上学时从家中出发,先向东走250米,再向北走50米就到达学校.