题目内容
6.已知a=$\frac{1}{3}$,化简求值:$\frac{1}{a}$-$\sqrt{{a}^{2}+\frac{1}{{a}^{2}}-2}$.分析 首先根据完全平方公式对被开方数变形,然后利用二次根式的性质化简,代入求值即可.
解答 解:原式=$\frac{1}{a}$-$\sqrt{(a-\frac{1}{a})^{2}}$=$\frac{1}{a}$-|a-$\frac{1}{a}$|=$\frac{1}{a}$-($\frac{1}{a}$-a)=a=$\frac{1}{3}$.
点评 此题主要考查的是二次根式的性质以及完全平方公式,注意$\sqrt{{a}^{2}}$=|a|=$\left\{\begin{array}{l}{a(a≥0)}\\{-a(a<0)}\end{array}\right.$,对a的符号的确定是关键.

练习册系列答案
相关题目
 如图是由A,B,C,D,E,五个正方形和长方形F组成的一个大长方形,其中A的边长为1,B的边长为x,试用x表示这个大长方形的面积.
如图是由A,B,C,D,E,五个正方形和长方形F组成的一个大长方形,其中A的边长为1,B的边长为x,试用x表示这个大长方形的面积.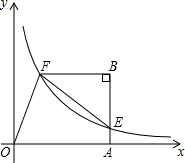 如图,四边形OABF中,∠OAB=∠B=90°,点A在x轴上,双曲线y=$\frac{k}{x}$过点F,交AB于点E,连接EF.若$\frac{BF}{OA}=\frac{2}{3}$,S△BEF=4,则k的值为( )
如图,四边形OABF中,∠OAB=∠B=90°,点A在x轴上,双曲线y=$\frac{k}{x}$过点F,交AB于点E,连接EF.若$\frac{BF}{OA}=\frac{2}{3}$,S△BEF=4,则k的值为( )