题目内容
16.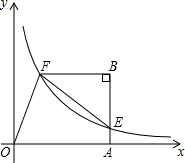 如图,四边形OABF中,∠OAB=∠B=90°,点A在x轴上,双曲线y=$\frac{k}{x}$过点F,交AB于点E,连接EF.若$\frac{BF}{OA}=\frac{2}{3}$,S△BEF=4,则k的值为( )
如图,四边形OABF中,∠OAB=∠B=90°,点A在x轴上,双曲线y=$\frac{k}{x}$过点F,交AB于点E,连接EF.若$\frac{BF}{OA}=\frac{2}{3}$,S△BEF=4,则k的值为( )| A. | 6 | B. | 8 | C. | 12 | D. | 16 |
分析 由于$\frac{BF}{OA}=\frac{2}{3}$,可以设F(m,n)则OA=3m,BF=2m,由于S△BEF=4,则BE=$\frac{4}{m}$,然后即可求出E(3m,n-$\frac{4}{m}$),依据mn=3m(n-$\frac{4}{m}$)可求mn=6,即求出k的值.
解答 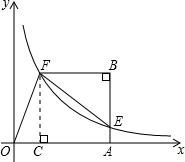 解:如图,过F作FC⊥OA于C,
解:如图,过F作FC⊥OA于C,
∵$\frac{BF}{OA}=\frac{2}{3}$,
∴OA=3OC,BF=2OC
∴若设F(m,n)
则OA=3m,BF=2m
∵S△BEF=4
∴BE=$\frac{4}{m}$
则E(3m,n-$\frac{4}{m}$)
∵E在双曲线y=$\frac{k}{x}$上
∴mn=3m(n-$\frac{4}{m}$)
∴mn=6
即k=6.
故选:A.
点评 此题主要考查了反比例函数的图象和性质、用坐标表示线段长和三角形面积,表示出E点坐标是解题关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
7.下列说法正确的是( )
| A. | 各边都相等的多边形是正多边形 | |
| B. | 各角都相等的多边形是正多边形 | |
| C. | 各边相等,各角也相等的多边形是正多边形 | |
| D. | 一个n边形(n>3)有n条边,n个内角,n条对角线 |