题目内容
18.若关于x的一元二次方程x2+6x-p=0有两个相等的实数根,则p=-9.分析 根据根的判别式得出△=0,代入即可得出关于p的方程,求出方程的解即可.
解答 解:∵关于x的一元二次方程x2+6x-p=0有两个相等的实数根,
∴△=62-4×1×(-p)=0,
解得:p=-9,
故答案为:-9.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式△=b2-4ac,当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
13. 如图,点C在线段AB上,点D是AC的中点,如果CB=$\frac{3}{2}$CD,AB=7cm,那么BC的长为( )
如图,点C在线段AB上,点D是AC的中点,如果CB=$\frac{3}{2}$CD,AB=7cm,那么BC的长为( )
 如图,点C在线段AB上,点D是AC的中点,如果CB=$\frac{3}{2}$CD,AB=7cm,那么BC的长为( )
如图,点C在线段AB上,点D是AC的中点,如果CB=$\frac{3}{2}$CD,AB=7cm,那么BC的长为( )| A. | 3cm | B. | 3.5cm | C. | 4cm | D. | 4.5cm |
10.下面说法正确的是( )
| A. | 一个人的体重与他的年龄成正比例关系 | |
| B. | 正方形的面积和它的边长成正比例关系 | |
| C. | 车辆所行驶的路程S一定时,车轮的半径r和车轮旋转的周数m成反比例关系 | |
| D. | 水管每分钟流出的水量Q一定时,流出的总水量y和放水的时间x成反比例关系 |
7. 小亮和小明沿同一条路同时从学校出发到市图书馆,学校与图书馆的路程是4千米,小亮骑自行车,小明步行,当小亮从原路回到学校时,小明刚好到达市图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分)之间的函数关系,根据图象提供信息,下列结论错误的是( )
小亮和小明沿同一条路同时从学校出发到市图书馆,学校与图书馆的路程是4千米,小亮骑自行车,小明步行,当小亮从原路回到学校时,小明刚好到达市图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分)之间的函数关系,根据图象提供信息,下列结论错误的是( )
 小亮和小明沿同一条路同时从学校出发到市图书馆,学校与图书馆的路程是4千米,小亮骑自行车,小明步行,当小亮从原路回到学校时,小明刚好到达市图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分)之间的函数关系,根据图象提供信息,下列结论错误的是( )
小亮和小明沿同一条路同时从学校出发到市图书馆,学校与图书馆的路程是4千米,小亮骑自行车,小明步行,当小亮从原路回到学校时,小明刚好到达市图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分)之间的函数关系,根据图象提供信息,下列结论错误的是( )| A. | 小亮在图书馆停留的时间是15分钟 | |
| B. | 小亮从学校去图书馆的速度和从图书馆返回学校的速度相同 | |
| C. | 小明离开学校的路程s(千米)与时间t(分)之间的函数关系式为S=$\frac{4}{45}$t | |
| D. | BC段s(千米)与t(分)之间的函数关系式为S=$\frac{4}{45}$t+12 |
8.若a<3,则化简$\sqrt{{a^2}-6a+9}$+|4-a|的结果是( )
| A. | -1 | B. | 1 | C. | 2a-7 | D. | 7-2a |
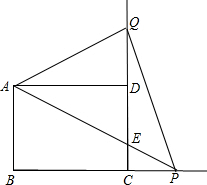 如图,已知矩形ABCD中,AB=4cm,BC=6cm,动点P从点C开始,以1cm/s的速度在BC的延长线上向右匀速运动,连接AP交CD边于点E,把射线AP沿直线AD翻折,交CD的延长线于点Q,设点P的运动时间为t.
如图,已知矩形ABCD中,AB=4cm,BC=6cm,动点P从点C开始,以1cm/s的速度在BC的延长线上向右匀速运动,连接AP交CD边于点E,把射线AP沿直线AD翻折,交CD的延长线于点Q,设点P的运动时间为t.