题目内容
19.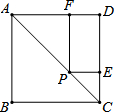 如图,在正方形ABCD中,对角线AC=6,点P是对角线AC上的一点,过点P作PF⊥AD,PE⊥CD,则PF+PE的值为( )
如图,在正方形ABCD中,对角线AC=6,点P是对角线AC上的一点,过点P作PF⊥AD,PE⊥CD,则PF+PE的值为( )| A. | 3$\sqrt{2}$ | B. | 3 | C. | 2$\sqrt{3}$ | D. | 6 |
分析 由正方形的性质得出∠PAF=∠PCE=45°,证出△APF和△CPE是等腰直角三角形,得出PF=$\frac{\sqrt{2}}{2}$AP,PE=$\frac{\sqrt{2}}{2}$PC,即可得出结论.
解答 解:∵四边形ABCD是正方形,
∴∠BAD=∠BCD=90°,∠PAF=∠PCE=45°,
∵PF⊥AD,PE⊥CD,
∴△APF和△CPE是等腰直角三角形,
∴PF=$\frac{\sqrt{2}}{2}$AP,PE=$\frac{\sqrt{2}}{2}$PC,
∴PF+PE=$\frac{\sqrt{2}}{2}$(AP+PC)=$\frac{\sqrt{2}}{2}$AC=3$\sqrt{2}$;
故选:A.
点评 本题考查了正方形的性质、等腰直角三角形的判定与性质、解直角三角形;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.一组数据:3,5,8,2,3,5的中位数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
9. 如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是( )
如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是( )
 如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是( )
如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
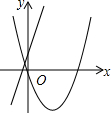
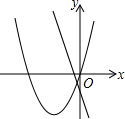
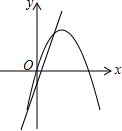
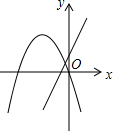
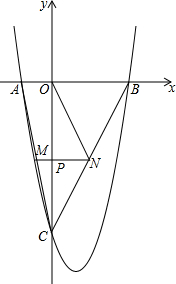 如图,抛物线y=x2+bx+c与x轴交于A(-2,0),B(6,0)两点,与y轴交于点C,请解答下列问题:
如图,抛物线y=x2+bx+c与x轴交于A(-2,0),B(6,0)两点,与y轴交于点C,请解答下列问题: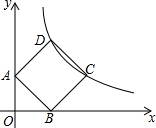 如图,正方形ABCD的顶点A、B分别在y正半轴和x正半轴上,顶点C、D在第一象限内反比例函数y=$\frac{k}{x}$的图象上.
如图,正方形ABCD的顶点A、B分别在y正半轴和x正半轴上,顶点C、D在第一象限内反比例函数y=$\frac{k}{x}$的图象上.