题目内容
19.已知菱形的周长为24cm,且有一个内角为60°,则该菱形的面积是18$\sqrt{3}$cm2.分析 首先根据题意画出图形,然后过点D作DE⊥AB于点E,由菱形的周长为24cm,可求得其边长,又由有一个内角为60°,可求得其高,继而求得答案.
解答 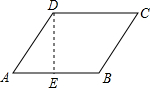 解:如图,过点D作DE⊥AB于点E,∠A=60°,
解:如图,过点D作DE⊥AB于点E,∠A=60°,
∵菱形的周长为24cm,
∴AB=AD=6cm,
∵在Rt△ADE中,∠A=60°,
∴∠ADE=30°,
∴AE=$\frac{1}{2}$AD=3cm,
∴DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=3$\sqrt{3}$(cm),
∴该菱形的面积是:AB•DE=18$\sqrt{3}$cm2.
故答案为:18$\sqrt{3}$cm2.
点评 此题考查了菱形的性质、含30°角的直角三角形的性质以及勾股定理.注意菱形的四条边都相等.

练习册系列答案
相关题目
7.已知分式$\frac{x-1}{2x}$的值为零,那么x的值是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 1 | D. | -1 |
8.直线y=kx+b-1不经过第二象限,则k,b的情况是( )
| A. | k>0,b>1 | B. | k>0,b≤1 | C. | k<0,b>1 | D. | k<0,b≥1 |
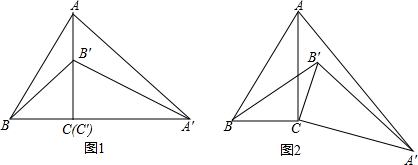
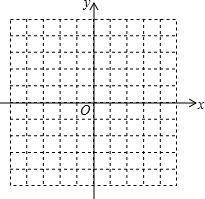 已知在等腰△ABC中,AB=AC,对称轴为x轴,点A的坐标为(-3,0),点B的坐标为(1,3).
已知在等腰△ABC中,AB=AC,对称轴为x轴,点A的坐标为(-3,0),点B的坐标为(1,3).