题目内容
15.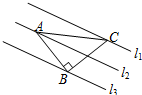 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3,上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC的长是$\sqrt{68}$.
如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3,上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC的长是$\sqrt{68}$.
分析 过A、C点作l3的垂线构造出直角三角形,根据三角形全等和勾股定理求出BC的长,再利用勾股定理即可求出.
解答 解:作AD⊥l3于D,作CE⊥l3于E,
∵∠ABC=90°,
∴∠ABD+∠CBE=90°,
又∵∠DAB+∠ABD=90°,
∴∠BAD=∠CBE,
又∵AB=BC,∠ADB=∠BEC,
在△ABD与△BCE中,
$\left\{\begin{array}{l}{∠BAD=∠CBE}\\{∠ADB=∠BEC}\\{AB=BC}\end{array}\right.$,
∴△ABD≌△BCE(AAS),
∴BE=AD=3,CE=2+3=5,
在Rt△BCE中,根据勾股定理,得BC=$\sqrt{{3}^{2}+{5}^{2}}=\sqrt{34}$,
在Rt△ABC中,根据勾股定理,得AC=$\sqrt{34+34}=\sqrt{68}$,
故答案为:$\sqrt{68}$
点评 本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.

练习册系列答案
相关题目
6.合肥市花卉种植专业户王有才承包了30亩花圃,分别种植康乃馨和玫瑰花,有关成本、销售额见下表:
(1)2014年,小王种植康乃馨和玫瑰花的总成本共计68万元,他种植康乃馨和玫瑰花各多少亩?
(2)2015年,小王继续用这30亩花圃全部种植康乃馨和玫瑰花,计划揉入成本不超过70万元,若每亩种植的成本,销售额与2014年相同.要获得最大利益,他应种植康乃馨和玫瑰花各多少亩?(收益=销售额-成本)
| 种植种类 | 成本(万元/亩) | 销售额(万元/亩) |
| 康乃馨 | 2.4 | 3 |
| 玫瑰花 | 2 | 2.5 |
(2)2015年,小王继续用这30亩花圃全部种植康乃馨和玫瑰花,计划揉入成本不超过70万元,若每亩种植的成本,销售额与2014年相同.要获得最大利益,他应种植康乃馨和玫瑰花各多少亩?(收益=销售额-成本)
5.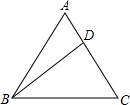 如图,在△ABC中,AB=AC=10,BC=12,有一点D在AC上移动,则AD+BD+CD的最小值是( )
如图,在△ABC中,AB=AC=10,BC=12,有一点D在AC上移动,则AD+BD+CD的最小值是( )
 如图,在△ABC中,AB=AC=10,BC=12,有一点D在AC上移动,则AD+BD+CD的最小值是( )
如图,在△ABC中,AB=AC=10,BC=12,有一点D在AC上移动,则AD+BD+CD的最小值是( )| A. | 18 | B. | 18.6 | C. | 20 | D. | 19.6 |
 已知:如图,AB=AD,∠D=∠B,∠1=∠2,求证:
已知:如图,AB=AD,∠D=∠B,∠1=∠2,求证: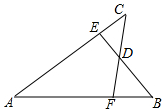 如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )
如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )