题目内容
12.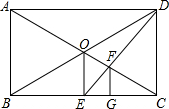 如图所示,在矩形ABCD中,对角线AC,BD相交于点O.过点O作OE⊥BC于点E,连接DE交OC于点F,过点F作FG⊥BC于点G,则△ABC与△FGC是位似图形吗?若是,请说出位似中心,并求出相似比;若不是,请说明理由.
如图所示,在矩形ABCD中,对角线AC,BD相交于点O.过点O作OE⊥BC于点E,连接DE交OC于点F,过点F作FG⊥BC于点G,则△ABC与△FGC是位似图形吗?若是,请说出位似中心,并求出相似比;若不是,请说明理由.
分析 根据三角形中位线定理证明△ABC与△FGC是位似图形,根据相似三角形的性质求出相似比.
解答 解:△ABC与△FGC是位似图形,
∵OE⊥BC,FG⊥BC,
∴OE∥FG,又OF、EG的连线相交于点C,
∴△ABC与△FGC是位似图形,位似中心是点C,
∵四边形ABCD是矩形,
∴∠BCD=90°,OB=OD,又OE⊥BC,
∴OE∥CD,
∴OE是△BCD的中位线,
∴OE=$\frac{1}{2}$CD,
∵OE∥CD,
∴$\frac{OF}{FC}$=$\frac{OE}{CD}$=$\frac{1}{2}$,则$\frac{CF}{CO}$=$\frac{2}{3}$,
∴△ABC与△FGC的相似比是3.
点评 本题考查的是位似变换的概念,如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 抛物线的部分图象如图所示,请确定该抛物线的解析式,并回答下列问题:
抛物线的部分图象如图所示,请确定该抛物线的解析式,并回答下列问题: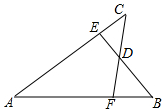 如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )
如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )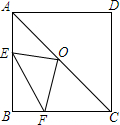 如图,边长为4cm的正方形ABCD,对角线AC,BD相交于点O,E是AB边上一动点(与A.B不重合),过点O作OF⊥OE交BC边于F.
如图,边长为4cm的正方形ABCD,对角线AC,BD相交于点O,E是AB边上一动点(与A.B不重合),过点O作OF⊥OE交BC边于F. 如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=$\frac{1}{2}$,且经过点(2,0),下列说法:
如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=$\frac{1}{2}$,且经过点(2,0),下列说法: