题目内容
19．
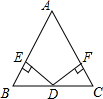如图，已知在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E，F．（1）求证：DE=DF；
（2）若AB=6，DE=3，求△ABC的面积．
分析 （1）首先连接AD，由AB=AC，D是BC的中点，根据三线合一的性质，可得∠EAD=∠FAD，再根据角平分线的性质即可证得DE=DF；
（2）根据三角形的面积公式进行计算即可．
解答 解：（1）如图，连接AD，
∵AB=AC，D是BC的中点，
∴∠EAD=∠FAD，
∵DE⊥AB，DF⊥AC，垂足分别为E、F，
∴DE=DF；
（2）△ABD的面积=$\frac{1}{2}AB•DE=\frac{1}{2}×6×3=9$，
所以△ABC的面积=2×9=18．
点评 本题考查了等腰三角形的性质、角平分线的性质，关键是根据等腰三角形的性质解答．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
已知：如图，AB=AD，∠D=∠B，∠1=∠2，求证：
已知：点D在AB上，点E在AC上，BE⊥AC，CD⊥AB，AB=AC，求证：∠B=∠C．