题目内容
16.已知点A(0,-a),B(b,0),如图1,有理数a,b满足a2+b2+8a-8b+32=0.(1)若点C(0,1),点D是第一象限内的点,连接DC交AB于点E.如图1,已知点E为线段DC中点,△ADC的面积=3,求点D的坐标;
(2)如图2,点G(2,0),连接AG,作∠BGH=∠AGO,点H为线段AB上一点,连接OH,试探究线段AG,GH,OH之间的关系.并正明你的结论.
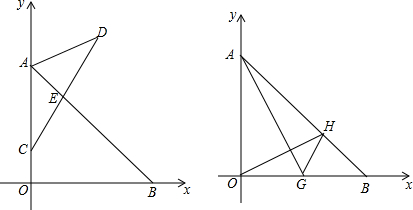
分析 (1)先求得A、B的坐标,作DH⊥y轴于H,作EF⊥y轴于F,根据三角形的面积求得DH=2,然后根据三角形中位线定理求得EF=1,由A、B的坐标,根据待定系数法求得直线AB的解析式,进而求得E的纵坐标,得出CF=2,即可求得FH=FC=2,得出D的纵坐标;
(2)作HM⊥OB于M,由∠BGH=∠AGO,根据直角三角函数得出$\frac{OA}{OG}$=$\frac{HM}{GM}$=2,设GM=m,则HM=2m,
进而得出2m=2-m,解得m=$\frac{2}{3}$,得出H的坐标,然后根据勾股定理分别求得AG、GH、OH的值,即可求得AG=GH+OH.
解答 解:∵有理数a,b满足a2+b2+8a-8b+32=0.
∴(a+4)2+(b-4)2=0,
∴a=-4,b=4,
∴A(0,4),B(4,0),
∴OA=4,OB=4,
(1)作DH⊥y轴于H
∵点C(0,1),
∴OC=1,
∴AC=3,
∵点E为线段DC中点,△ADC的面积=3,
∴$\frac{1}{2}$AC•DH=3,
∴DH=2,
作EF⊥y轴于F,
∴EF∥DH,
∵点E为线段DC中点,
∴EF=1,
由A(0,4),B(4,0)的直线AB为y=-x+4,
∴yE=3,
∴E(1,3),
∴OF=3,
∴EC=2,
∴HF=2,
∴OH=5
∴D(2,5);
(2)AG=GH+OH;
作HM⊥OB于M,
∵∠BGH=∠AGO,
∴$\frac{OA}{OG}$=$\frac{HM}{GM}$,
∵OA=4,OG=2,
∴$\frac{HM}{GM}$=2,
设GM=m,则HM=2m,
∵OA=OB=4,
∴△AOB是等腰直角三角形,
∴∠B=45°,
∴△HMB是等腰直角三角形,
∴HM=BM=2-m,
∴2m=2-m,解得m=$\frac{2}{3}$,
∴H($\frac{8}{3}$,$\frac{4}{3}$),
∵A(0,4),G(2,0),
∴AG=2$\sqrt{5}$,GH=$\frac{2}{3}$$\sqrt{5}$,OH=$\frac{4}{3}$$\sqrt{5}$,
∴AG=GH+OH.
点评 本题是一次函数的综合题,考查了待定系数法求一次函数的解析式,三角形的中位线定理,直角三角函数,勾股定理的应用以及等腰三角形的判定和性质,作出辅助线构建直角三角形,求得点的坐标是解题的关键.

| 种植种类 | 成本(万元/亩) | 销售额(万元/亩) |
| 康乃馨 | 2.4 | 3 |
| 玫瑰花 | 2 | 2.5 |
(2)2015年,小王继续用这30亩花圃全部种植康乃馨和玫瑰花,计划揉入成本不超过70万元,若每亩种植的成本,销售额与2014年相同.要获得最大利益,他应种植康乃馨和玫瑰花各多少亩?(收益=销售额-成本)
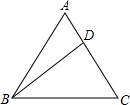 如图,在△ABC中,AB=AC=10,BC=12,有一点D在AC上移动,则AD+BD+CD的最小值是( )
如图,在△ABC中,AB=AC=10,BC=12,有一点D在AC上移动,则AD+BD+CD的最小值是( )| A. | 18 | B. | 18.6 | C. | 20 | D. | 19.6 |
| A. | 1-4(2x-3)=-5 | B. | 1-4(2x-3)=5 | C. | 2x-3-4=-5 | D. | 2x-3-4=5(2x-3) |