题目内容
10. 如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是( )
如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是( )| A. | $\frac{1}{2}$π-1 | B. | $\frac{1}{2}$π-2 | C. | π-2 | D. | π-1 |
分析 已知BC为直径,则∠CDB=90°,在等腰直角三角形ABC中,CD垂直平分AB,CD=DB,D为半圆的中点,阴影部分的面积可以看做是扇形ACB的面积与△ADC的面积之差.
解答 解:在Rt△ACB中,AB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∵BC是半圆的直径,
∴∠CDB=90°,
在等腰Rt△ACB中,CD垂直平分AB,CD=BD=$\sqrt{2}$,
∴D为半圆的中点,
∴S阴影部分=S扇形ACB-S△ADC=$\frac{1}{4}$π×22-$\frac{1}{2}$×($\sqrt{2}$)2=π-1.
故选D.
点评 本题主要考查扇形面积的计算,在解答此题时要注意不规则图形面积的求法.

练习册系列答案
相关题目
20.以下问题,不适合用全面调查的是( )
| A. | 了解一批灯泡的使用寿命 | B. | 学校招聘教师,对应聘人员的面试 | ||
| C. | 了解全校学生的课外读书时间 | D. | 旅客上飞机前的安检 |
5.下列计算正确的是( )
| A. | a•a3=a3 | B. | a4+a3=a2 | C. | (a2)5=a7 | D. | (-ab)2=a2b2 |
2.某校学生小明每天骑自行车上学时都要经过一个十字路口,设十字路口有红、黄、绿三色交通信号灯,他在路口遇到红灯的概率为$\frac{1}{3}$,遇到黄灯的概率为$\frac{1}{9}$,那么他遇到绿灯的概率为( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
11.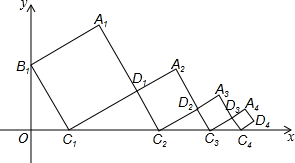 如图,平面直角坐标系中放置了四个正方形,其中相邻两个正方形的两边在同一直线上,已知正方形A1B1C1D1的边长为1,∠OC1B1=60°.若按此规律排列,第2015个小正方形最上面的顶点A2015的纵坐标是( )
如图,平面直角坐标系中放置了四个正方形,其中相邻两个正方形的两边在同一直线上,已知正方形A1B1C1D1的边长为1,∠OC1B1=60°.若按此规律排列,第2015个小正方形最上面的顶点A2015的纵坐标是( )
 如图,平面直角坐标系中放置了四个正方形,其中相邻两个正方形的两边在同一直线上,已知正方形A1B1C1D1的边长为1,∠OC1B1=60°.若按此规律排列,第2015个小正方形最上面的顶点A2015的纵坐标是( )
如图,平面直角坐标系中放置了四个正方形,其中相邻两个正方形的两边在同一直线上,已知正方形A1B1C1D1的边长为1,∠OC1B1=60°.若按此规律排列,第2015个小正方形最上面的顶点A2015的纵坐标是( )| A. | ($\frac{\sqrt{3}}{3}$)2014×($\frac{1+\sqrt{3}}{2}$) | B. | ($\frac{\sqrt{3}}{3}$)2015($\frac{1+\sqrt{3}}{2}$) | C. | ($\frac{\sqrt{3}}{2}$)2014×($\frac{1+\sqrt{3}}{3}$) | D. | ($\frac{\sqrt{3}}{2}$)2015×($\frac{1+\sqrt{3}}{3}$) |
 如图,Rt△ABC中,∠B=90°,AB=4,BC=3,AC的垂直平分线DE分别交AB,AC于D,E两点,则CD的长为$\frac{25}{8}$.
如图,Rt△ABC中,∠B=90°,AB=4,BC=3,AC的垂直平分线DE分别交AB,AC于D,E两点,则CD的长为$\frac{25}{8}$.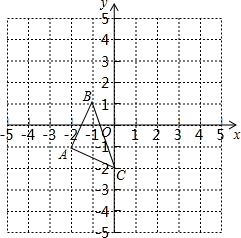 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,-1)、B(-1,1)、C(0,-2).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,-1)、B(-1,1)、C(0,-2).