题目内容
15. 如图,Rt△ABC中,∠B=90°,AB=4,BC=3,AC的垂直平分线DE分别交AB,AC于D,E两点,则CD的长为$\frac{25}{8}$.
如图,Rt△ABC中,∠B=90°,AB=4,BC=3,AC的垂直平分线DE分别交AB,AC于D,E两点,则CD的长为$\frac{25}{8}$.
分析 先根据线段垂直平分线的性质得出CD=AD,故AB=BD+AD=BD+CD,设CD=x,则BD=4-x,在Rt△BCD中根据勾股定理求出x的值即可.
解答 解:∵DE是AC的垂直平分线,
∴CD=AD,
∴AB=BD+AD=BD+CD,
设CD=x,则BD=4-x,
在Rt△BCD中,
CD2=BC2+BD2,即x2=32+(4-x)2,
解得x=$\frac{25}{8}$.
故答案为:$\frac{25}{8}$.
点评 本题考查的是线段垂直平分线的性质,熟知垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
相关题目
6.下列各数中没有平方根的是( )
| A. | 0 | B. | -82 | C. | (-$\frac{1}{4}$)2 | D. | -(-3) |
10. 如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是( )
如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是( )
 如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是( )
如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是( )| A. | $\frac{1}{2}$π-1 | B. | $\frac{1}{2}$π-2 | C. | π-2 | D. | π-1 |
20.-3的绝对值是( )
| A. | -3 | B. | 3 | C. | -3-1 | D. | 3-1 |
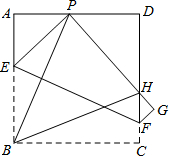 如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.现给出以下四个命题
如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.现给出以下四个命题