题目内容
10.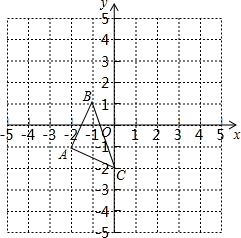 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,-1)、B(-1,1)、C(0,-2).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,-1)、B(-1,1)、C(0,-2).(1)点A关于坐标原点O对称的点的坐标为(2,1);
(2)将△ABC绕点C顺时针旋转90°,画出旋转后得到的△A1B1C;
(3)在(2)中,求边CB旋转过程中所扫过区域的面积是多少?(结果保留π).
分析 (1)利用关于原点对称点的性质,直接得出答案;
(2)利用旋转的性质分别得出B1,A1的位置,进而得出答案;
(3)利用勾股定理得出扇形半径,再利用扇形面积求法得出答案.
解答  解:(1)∵A(-2,-1),
解:(1)∵A(-2,-1),
∴点A关于坐标原点O对称的点的坐标为:(2,1);
故答案为:(2,1);
(2)如图所示:△A1B1C,即为所求;
(3)边CB旋转过程中所扫过区域的面积是:$\frac{90π×(\sqrt{10})^{2}}{180}$=5π.
点评 此题主要考查了旋转变换以及扇形面积求法,根据题意得出BC所扫过区域是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.下列四个多项式中,能因式分解的是( )
| A. | a2+1 | B. | a2-2a+1 | C. | x2+5y | D. | x2-5y |
10. 如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是( )
如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是( )
 如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是( )
如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是( )| A. | $\frac{1}{2}$π-1 | B. | $\frac{1}{2}$π-2 | C. | π-2 | D. | π-1 |
2.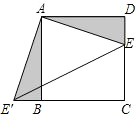 如图,在正方形ABCD中,AB=3,点E在CD边上,DE=1,把△ADE绕点A顺时针旋转90°,得到△ABE′,连接EE′,则线段EE′的长为( )
如图,在正方形ABCD中,AB=3,点E在CD边上,DE=1,把△ADE绕点A顺时针旋转90°,得到△ABE′,连接EE′,则线段EE′的长为( )
 如图,在正方形ABCD中,AB=3,点E在CD边上,DE=1,把△ADE绕点A顺时针旋转90°,得到△ABE′,连接EE′,则线段EE′的长为( )
如图,在正方形ABCD中,AB=3,点E在CD边上,DE=1,把△ADE绕点A顺时针旋转90°,得到△ABE′,连接EE′,则线段EE′的长为( )| A. | $2\sqrt{5}$ | B. | $2\sqrt{3}$ | C. | 4 | D. | $2\sqrt{10}$ |
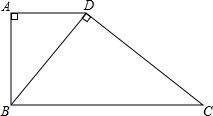 已知,如图,梯形ABCD中,AD∥BC,∠A=90°,BC=10,CD=8,对角线BD⊥CD.
已知,如图,梯形ABCD中,AD∥BC,∠A=90°,BC=10,CD=8,对角线BD⊥CD.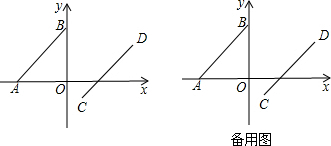
 如图所示,已知AD是△ABC的角平分线,且∠ADC=2∠B,∠C=75°,求∠BAC与∠B的度数.
如图所示,已知AD是△ABC的角平分线,且∠ADC=2∠B,∠C=75°,求∠BAC与∠B的度数.