题目内容
3.在四边形ABCD中,AD∥BC,AB⊥BC,AD=4,将线段CD以D为中心逆时针旋转90°至DE,连接AE,CE,△ADE的面积为6,则BC的长为7或1.分析 此题在旋转的基础上,巧妙作辅助线:作DG⊥BC于G,作EF⊥AD于F.构造全等三角形和矩形,根据全等三角形的性质和矩形的性质进行计算.
解答  解:
解:
①当AD<BC时,如图,作DG⊥BC于G,作EF⊥AD于F.得矩形ABGD,则BG=AD=4.
∵△ADE的面积为6.
∴EF=3.
根据旋转的性质,可知DE=DC,DE⊥DC,∠CDG=∠EDF,
在△CDG和△EDF中
$\left\{\begin{array}{l}{∠CDG=∠EDF}\\{∠DGC=∠EFD}\\{DE=CD}\end{array}\right.$
∴△CDG≌△EDF(AAS),
∴EF=GC=3,
∴BC=BG+GC=4+3=7;
②当AD>BC时,同理可求得BC=1,
故答案为:7或1.
点评 本题考查了旋转的性质的运用,直角梯形的性质的运用.关键是通过DC、DE的旋转关系,作出旋转的三角形.

练习册系列答案
相关题目
14.某同学骑车从学校到家,每分行1.5千米,某天回家时,速度提高到每分行2千米,结果提前5分回家,设原来从学校到家之间骑车用x分,则列方程为( )
| A. | 1.5x=2(x+5) | B. | 1.5x=2(x-5) | C. | 1.5(x+5)=2x | D. | 1.5(x-5)=2x |
8.一艘轮船以16n mile/h的速度从港口A出发向东北方向航行,另一轮船以12n mile/h的速度从港口A出发向东南方向航行,则3h后两船相距( )
| A. | 36n mile | B. | 48n mile | C. | 60n mile | D. | 54n mile |
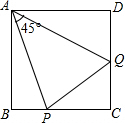 如图,在正方形ABCD中,P、Q分别为BC、CD边上的点,且∠PAQ=45°,△PCQ的周长为4,正方形ABCD的边长是多少?
如图,在正方形ABCD中,P、Q分别为BC、CD边上的点,且∠PAQ=45°,△PCQ的周长为4,正方形ABCD的边长是多少?