题目内容
11.某人沿坡角为30°的斜坡上山,行了1000m到达山顶,求山高和行进的水平距离.(参考数据:$\sqrt{3}$≈1.732).分析 在三角函数中,根据坡度角的正弦值=垂直高度:坡面距离即可解答.
解答  解:由已知得:如图,∠A=30°,∠C=90°,
解:由已知得:如图,∠A=30°,∠C=90°,
则山高度BC=ABsin30°=1000×$\frac{1}{2}$=500(米).
行进的水平距离为:$\sqrt{3}$BC=500$\sqrt{3}$=866米,
所以山高为500米,行进的水平距离为866米.
点评 此题主要考查了坡角问题的应用,通过构造直角三角形,利用锐角三角函数求解是解题关键.

练习册系列答案
相关题目
19. 如图,在△ABC中,∠C=90°,AC=BC=a,分别以点A、B、C为圆心,a为半径$\widehat{CE}$、$\widehat{CD}$、$\widehat{AB}$,设$\widehat{CE}$与$\widehat{CD}$的长度之和为l1,$\widehat{AB}$的长为l2,则l1与l2的大小关系为( )
如图,在△ABC中,∠C=90°,AC=BC=a,分别以点A、B、C为圆心,a为半径$\widehat{CE}$、$\widehat{CD}$、$\widehat{AB}$,设$\widehat{CE}$与$\widehat{CD}$的长度之和为l1,$\widehat{AB}$的长为l2,则l1与l2的大小关系为( )
 如图,在△ABC中,∠C=90°,AC=BC=a,分别以点A、B、C为圆心,a为半径$\widehat{CE}$、$\widehat{CD}$、$\widehat{AB}$,设$\widehat{CE}$与$\widehat{CD}$的长度之和为l1,$\widehat{AB}$的长为l2,则l1与l2的大小关系为( )
如图,在△ABC中,∠C=90°,AC=BC=a,分别以点A、B、C为圆心,a为半径$\widehat{CE}$、$\widehat{CD}$、$\widehat{AB}$,设$\widehat{CE}$与$\widehat{CD}$的长度之和为l1,$\widehat{AB}$的长为l2,则l1与l2的大小关系为( )| A. | l1>l2 | B. | l1=l2 | C. | l1<l2 | D. | 不能确定 |
16.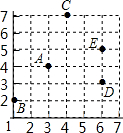 张萌在纸上画了一个如图所示的网格图,每个小格的边长都是1个单位长度,点A,B,C,D,E都在格点上,若张萌将点E表示成(6,5),则下列四点表示不正确的是( )
张萌在纸上画了一个如图所示的网格图,每个小格的边长都是1个单位长度,点A,B,C,D,E都在格点上,若张萌将点E表示成(6,5),则下列四点表示不正确的是( )
 张萌在纸上画了一个如图所示的网格图,每个小格的边长都是1个单位长度,点A,B,C,D,E都在格点上,若张萌将点E表示成(6,5),则下列四点表示不正确的是( )
张萌在纸上画了一个如图所示的网格图,每个小格的边长都是1个单位长度,点A,B,C,D,E都在格点上,若张萌将点E表示成(6,5),则下列四点表示不正确的是( )| A. | 点A表示成(3,4) | B. | 点B表示成(2,1) | C. | 点C表示成(4,7) | D. | 点D表示成(6,3) |
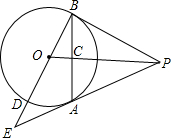 如图,PA为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点D,与PA的延长线交于点E.
如图,PA为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点D,与PA的延长线交于点E.
 已知⊙O的半径为1,A、B、C是⊙O上的三等分点,圆弧$\widehat{AOB}$,$\widehat{BOC}$,$\widehat{COA}$相交于O,则图中阴影部分面积是π-$\frac{3\sqrt{3}}{2}$.
已知⊙O的半径为1,A、B、C是⊙O上的三等分点,圆弧$\widehat{AOB}$,$\widehat{BOC}$,$\widehat{COA}$相交于O,则图中阴影部分面积是π-$\frac{3\sqrt{3}}{2}$.