题目内容
8.一艘轮船以16n mile/h的速度从港口A出发向东北方向航行,另一轮船以12n mile/h的速度从港口A出发向东南方向航行,则3h后两船相距( )| A. | 36n mile | B. | 48n mile | C. | 60n mile | D. | 54n mile |
分析 首先根据方向角得出∠BAC=90°,再利用勾股定理得出BC的长.
解答 解:∵一轮船以16n mi1e/h的速度从港口A出发向东北方向航行,
另一轮船以12n mi1e/h的速度同时从港口A出发向东南方向航行,
∴∠BAC=90°,离开港口A3h后,AB=48n mi1e,AC=36n mi1e,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=60(n mi1e).
答:3h后两船相距60n mi1e.
故选:C.
点评 此题主要考查了勾股定理的应用以及方向角问题,得出AB,AC的长是解题关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
16.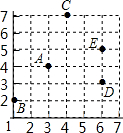 张萌在纸上画了一个如图所示的网格图,每个小格的边长都是1个单位长度,点A,B,C,D,E都在格点上,若张萌将点E表示成(6,5),则下列四点表示不正确的是( )
张萌在纸上画了一个如图所示的网格图,每个小格的边长都是1个单位长度,点A,B,C,D,E都在格点上,若张萌将点E表示成(6,5),则下列四点表示不正确的是( )
 张萌在纸上画了一个如图所示的网格图,每个小格的边长都是1个单位长度,点A,B,C,D,E都在格点上,若张萌将点E表示成(6,5),则下列四点表示不正确的是( )
张萌在纸上画了一个如图所示的网格图,每个小格的边长都是1个单位长度,点A,B,C,D,E都在格点上,若张萌将点E表示成(6,5),则下列四点表示不正确的是( )| A. | 点A表示成(3,4) | B. | 点B表示成(2,1) | C. | 点C表示成(4,7) | D. | 点D表示成(6,3) |
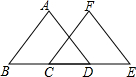 如图,点B、C、D、E在同一直线上,并且BC=DE.若AB=CF,AD=EF.试探索AB与FC的位置关系,并说明理由.
如图,点B、C、D、E在同一直线上,并且BC=DE.若AB=CF,AD=EF.试探索AB与FC的位置关系,并说明理由. 空调外机安装在墙壁上时,一般都会像如图所示的方法固定在墙壁上,这种方法是利用了三角形的稳定性.
空调外机安装在墙壁上时,一般都会像如图所示的方法固定在墙壁上,这种方法是利用了三角形的稳定性.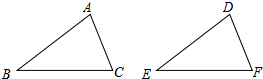 如图,给出下列四组条件:
如图,给出下列四组条件: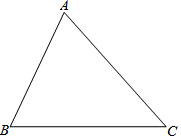 如图,在某城区地图上,有一块△ABC区域,市政规划要把△ABC区域划分成三个三角形小区域,使任何两个区域都相邻,并且使划分的三个小区域面积彼此相等.请你探究后,把符合题意的示意图画在图中,并说明所画的线是什么线.
如图,在某城区地图上,有一块△ABC区域,市政规划要把△ABC区域划分成三个三角形小区域,使任何两个区域都相邻,并且使划分的三个小区域面积彼此相等.请你探究后,把符合题意的示意图画在图中,并说明所画的线是什么线.