题目内容
10．当x=2时，式子2014-（x-2）2有最大值，最大值为2014；当y=-1时，式子y2+2y+5有最小值，值为4．分析 根据-（x-2）2≤0可知2014-（x-2）2≤2014可得最值情况；将y2+2y+5配方成（y+1）2+4可知最值情况．
解答 解：∵-（x-2）2≤0，
∴2014-（x-2）2≤2014，
∴当x=2时，式子2014-（x-2）2有最大值2014；
∵y2+2y+5=（y+1）2+4，且（y+1）2≥0，
∴（y+1）2+4≥4，
∴式子y2+2y+5当y=-1时，有最小值，最小值为4；
故答案为：2，2014，-1，小，4．
点评 本题主要考查配方法求函数或代数式的最值情况，熟练掌握完全平方公式是解题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目
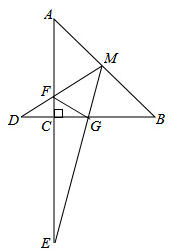如图，M为等腰直角三角形ABC斜边AB的中点，AC=4，MD交AC于F，交BC延长线于D，ME交BC于G，交AC延长线于E，且AF=3，∠DMG=45°．