题目内容
10.(1)计算:(-2)3+($\frac{1}{3}$)-1-|-5|+($\sqrt{3}$-2)0(2)先化简,再求值:$(1+\frac{1}{x-2})$÷$\frac{x^2-2x+1}{x^2-4}$,其中x=-5.
分析 (1)根据负整数指数幂和零指数幂的意义进行计算,即可得出结果;
(2)首先根据分式的混合运算进行计算化简,再代入求值即可,注意因式分解.
解答 解:(1)(-2)3+($\frac{1}{3}$)-1-|-5|+($\sqrt{3}$-2)0
=-8+3-5+1
=-9;
(2)$(1+\frac{1}{x-2})$÷$\frac{x^2-2x+1}{x^2-4}$,
=$\frac{x-2+1}{x-2}$×$\frac{(x+2)(x-2)}{(x-1)^{2}}$
=$\frac{x+2}{x-1}$
当x=-5时,
原式=$\frac{-5+2}{-5-1}$=$\frac{1}{2}$
点评 本题考查了负整数指数幂和零指数幂的意义、分式的化简求值、因式分解;熟练掌握负整数指数幂和零指数幂的意义、分式的化简求值是解决问题的关键.

练习册系列答案
相关题目
18.若a<b,则下列不等式的变形中不正确的是( )
| A. | a+5<b+5 | B. | $\frac{a}{5}$$<\frac{b}{5}$ | C. | 5a-1<5b-1 | D. | 5-a<5-b |
15.下列命题是真命题的是( )
| A. | 两条不相交的直线就是平行线 | |
| B. | 过任意一点可以作已知直线的一条平行线 | |
| C. | 过直线外任意一点作已知直线的垂线,可以作无数条 | |
| D. | 直线外一点与直线上各点所连接的所有线段中,垂线段最短 |
19.学校需要测量升旗杆的高度.同学们发现系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的长度未知.经测量,绳子多出的部分长度为2m,将绳子沿地面拉直,绳子底端距离旗杆底端6m,求旗杆的高度.
20.2015年盐城市中考考生约55800人,则数据55800用科学记数法可表示为( )
| A. | 0.558×105 | B. | 5.58×105 | C. | 5.58×104 | D. | 55.8×103 |
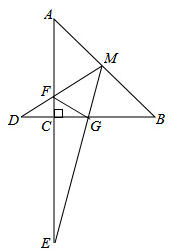 如图,M为等腰直角三角形ABC斜边AB的中点,AC=4,MD交AC于F,交BC延长线于D,ME交BC于G,交AC延长线于E,且AF=3,∠DMG=45°.
如图,M为等腰直角三角形ABC斜边AB的中点,AC=4,MD交AC于F,交BC延长线于D,ME交BC于G,交AC延长线于E,且AF=3,∠DMG=45°.