题目内容
16.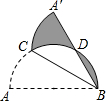 如图,点C在以AB为直径的半圆弧上,∠ABC=30°,沿直线CB将半圆折叠,点A落在点A′处,A′B和$\widehat{BC}$交于点D,已知AB=6,则图中阴影部分的面积为$\frac{3}{2}$π.
如图,点C在以AB为直径的半圆弧上,∠ABC=30°,沿直线CB将半圆折叠,点A落在点A′处,A′B和$\widehat{BC}$交于点D,已知AB=6,则图中阴影部分的面积为$\frac{3}{2}$π.
分析 连接AD,CD,根据折叠的性质得到∠ABC=∠CBA′=30°,AB=A′B=6,求得∠ABD=60°,根据圆周角定理得到∠ADB=90°,求得∠BAD=30°,得到$\widehat{AC}$=$\widehat{CD}$=$\widehat{BD}$,BD=$\frac{1}{2}$AB=A′B,根据扇形的面积公式即可得到结论.
解答 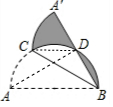 解:连接AD,CD,
解:连接AD,CD,
∵沿直线CB将半圆折叠,点A落在点A′处,
∴∠ABC=∠CBA′=30°,AB=A′B=6,
∴∠ABD=60°,
∵AB是半圆的直径,
∴∠ADB=90°,
∴∠BAD=30°,
∴$\widehat{AC}$=$\widehat{CD}$=$\widehat{BD}$,BD=$\frac{1}{2}$AB=A′B,
∴CD=BD=A′B,∠A′DC=60°,
∴图中阴影部分的面积=$\frac{60•π×{3}^{2}}{360}$=$\frac{3}{2}$π,
故答案为:$\frac{3}{2}$π.
点评 本题考查了扇形的面积的计算,圆周角定理,折叠的性质,正确的识别图形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
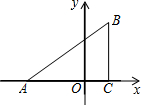 已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A、C的坐标分别为A(-3,0),C(1,0),$\frac{BC}{AC}$=$\frac{3}{4}$.
已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A、C的坐标分别为A(-3,0),C(1,0),$\frac{BC}{AC}$=$\frac{3}{4}$.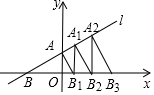 如图,在平面直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x+1交x轴于点B,交y轴于点A,过点A作AB1⊥AB交x轴于点B1,过点B1作B1A1⊥x轴交直线l于点A2…依次作下去,则点Bn的横坐标为$(\frac{4}{3})^{n}\sqrt{3}-\sqrt{3}$.
如图,在平面直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x+1交x轴于点B,交y轴于点A,过点A作AB1⊥AB交x轴于点B1,过点B1作B1A1⊥x轴交直线l于点A2…依次作下去,则点Bn的横坐标为$(\frac{4}{3})^{n}\sqrt{3}-\sqrt{3}$. 将一直角三角板与两边平行的纸条如图放置.已知∠1=30°,则∠2=60°.
将一直角三角板与两边平行的纸条如图放置.已知∠1=30°,则∠2=60°.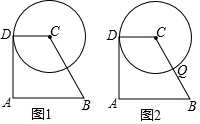 如图1,四边形ABCD中,AB∥CD,AB=2CD=2$\sqrt{3}$,AD=3,⊙C与AD相切于点D,P是线段AB上一动点,以点P为圆心,PB长为半径作⊙P.
如图1,四边形ABCD中,AB∥CD,AB=2CD=2$\sqrt{3}$,AD=3,⊙C与AD相切于点D,P是线段AB上一动点,以点P为圆心,PB长为半径作⊙P.