题目内容
20.在Rt△ABC中,∠C=90°,AB=13,AC=5.(1)以点A为圆心,4为半径的⊙A与直线BC的位置关系是相离;
(2)以点B为圆心的⊙B与直线AC相交,则⊙B的直径r的取值范围是r>12;
(3)以点C为圆心,R为半径的⊙C与直线AB相切,则R=$\frac{60}{13}$.
分析 (1)根据圆心到直线的距离大于圆的半径时直线与圆相离进行判断;
(2)先利用勾股定理计算出BC=12,再根据直线与圆相交的判定方法即可得到r>12;
(3)先利用面积法计算出CD,然后根据直线与圆相切的条件即可得到R的值.
解答 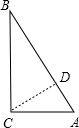 解:(1)∵AC⊥BC,
解:(1)∵AC⊥BC,
而AC>4,
∴以点A为圆心,4为半径的⊙A与直线BC相离;
(2)BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
∵BC⊥AC,
∴⊙B的半径大于BC时,以点B为圆心的⊙B与直线AC相交,
即r>12;
(3)作CD⊥AB于D,如图,
∵$\frac{1}{2}$CD•AB=$\frac{1}{2}$AC•BC,
∴CD=$\frac{5×12}{13}$=$\frac{60}{13}$,
当R=$\frac{60}{13}$时,以点C为圆心,R为半径的⊙C与直线AB相切.
故答案为相离,r>12,$\frac{60}{13}$.
点评 本题考查了直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,则直线l和⊙O相交?d<r;直线l和⊙O相切?d=r;直线l和⊙O相离?d>r.也考查了勾股定理.

练习册系列答案
相关题目
9.下列说法正确的是( )
| A. | 16的平方根是4 | B. | -1的平方根是-1 | ||
| C. | -2是4的一个平方根 | D. | (-1)2的平方根是-1 |
 如图,矩形草坪的长是30m,宽是10m,现要修建一条平行于草坪边缘的矩形小路,使得小路的形状与原来草坪的形状相似,求小路的宽.
如图,矩形草坪的长是30m,宽是10m,现要修建一条平行于草坪边缘的矩形小路,使得小路的形状与原来草坪的形状相似,求小路的宽. 如图,用下面的方法可以画△AOB的内接等边三角形,阅读后解答相应问题.
如图,用下面的方法可以画△AOB的内接等边三角形,阅读后解答相应问题.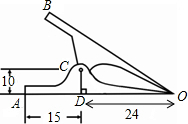 如图是一个常见铁夹的剖面图,OA,OB表示铁夹的两个面,C是轴,CD⊥OA,垂足为D,DA=15mm,DO=24mm,DC=10mm,且铁夹的剖面图是轴对称图形,求A,B两点间的距离.
如图是一个常见铁夹的剖面图,OA,OB表示铁夹的两个面,C是轴,CD⊥OA,垂足为D,DA=15mm,DO=24mm,DC=10mm,且铁夹的剖面图是轴对称图形,求A,B两点间的距离. 如图,平面直角坐标系中,点B的坐标为(4,2),过点B作y轴的垂线,垂足为A,连结OB,将△OAB沿OB折叠,使点A落在点A1处,A1B与x轴交与点F.
如图,平面直角坐标系中,点B的坐标为(4,2),过点B作y轴的垂线,垂足为A,连结OB,将△OAB沿OB折叠,使点A落在点A1处,A1B与x轴交与点F.