题目内容
2.已知不等式组$\left\{\begin{array}{l}{3(2x-1)<2x+8}\\{2+\frac{3(x+1)}{8}>3-\frac{x-1}{4}}\end{array}\right.$.(1)求这个不等式组的解集;
(2)若上述不等式的整数解满足方程a+6=x-2a,求a的值.
(3)求代数式a2014-$\frac{1}{{a}^{2015}}$的值.
分析 (1)先求出每个不等式的解集,再求出不等式组的解集即可;
(2)求出方程的解,即可得出关于a的不等式组,求出不等式组的解集即可;
(3)求出整数a=-1,代入求出即可.
解答 解:(1)$\left\{\begin{array}{l}{3(2x-1)<2x+8①}\\{2+\frac{3(x+1)}{8}>3-\frac{x-1}{4}②}\end{array}\right.$
∵解不等式①得:x<4,
解不等式②得:x>$\frac{7}{5}$,
∴不等式组的解集为$\frac{7}{5}$<x<4;
(2)a+6=x-2a,
x=6+3a,
即$\frac{7}{5}$<6+3a<4,
解得:-$\frac{23}{15}$<a<-$\frac{2}{3}$;
(3)∵-$\frac{23}{15}$<a<-$\frac{2}{3}$,
∴整数a=-1,
∴a2014-$\frac{1}{{a}^{2015}}$=(-1)2014-$\frac{1}{(-1)^{2015}}$=2.
点评 本题考查了解一元一次不等式组,解一元一次方程,不等式组的整数解的应用,能求出关于a的不等式组是解此题的关键,难度适中.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
13.设对任意实数x,用[x]表示不大于x的最大整数,则对任意实数x,y,有( )
| A. | -[-x]=[x] | B. | [2x]=2[x] | C. | [x+y]≤[x]+[y] | D. | [x-y]≤[x]-[y] |
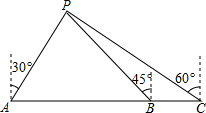 天宜号船向正东方航行(如图),船在A处时测得灯塔在P北偏东30°方向,前进到B处时测得灯塔P恰好在西北方向,又航行半小时到达C处,此时测得灯塔P在北偏西60°方向,若船速为每小时20海里,求A、C两点间的距离.
天宜号船向正东方航行(如图),船在A处时测得灯塔在P北偏东30°方向,前进到B处时测得灯塔P恰好在西北方向,又航行半小时到达C处,此时测得灯塔P在北偏西60°方向,若船速为每小时20海里,求A、C两点间的距离.