题目内容
3．
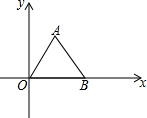如图，A，B两点的坐标分别是A（1，$\sqrt{3}$），B（$\sqrt{5}$，0），则△ABO的面积是$\frac{\sqrt{15}}{2}$．
分析 根据A点的坐标，我们可知三角形OAB的高应该是A点纵坐标的绝对值即1．根据B点的坐标我们可知三角形OAB的底边长应该是B点横坐标的绝对值即$\sqrt{5}$，于是根据三角形的面积公式即可求出△OAB的面积．
解答 解：根据题意可得：
三角形OAB的面积=$\frac{1}{2}$×$\sqrt{3}×\sqrt{5}$=$\frac{\sqrt{15}}{2}$．
故答案为：$\frac{\sqrt{15}}{2}$．
点评 本题考查了坐标与图形性质及三角形的面积的求法，根据点的坐标得出三角形的高和底的长是解题的关键．
练习册系列答案
相关题目
小明家离学校1880米，其中有一段为上坡路，另一段为下坡路，如图所示，他骑自行车去上学用了10分钟．已知小明在上坡路上的平均速度是6千米/时，下坡路上的平均速度为12千米/时，问小明在上学路上走上坡路、下坡路各用了多少分钟？
在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两墙足够长）用26m长的篱笆围成一个矩形花园ABCD（篱笆只围AB、BC两边），设AB=x m．
如图，AB是⊙O的弦，OC⊥AB，垂足为C．若AB=2$\sqrt{3}$，OC=1，则OB的长为2．
15．下列命题中，是真命题的有（ ）
| A． | 等角的余角角相等 | B． | 同位角相等 | ||
| C． | 若a2=b2，则a=b | D． | 相等角是对顶角 |
在平面直角坐标系中，若横坐标、纵坐标均为整数点称为格点，若一个多边形的顶点都是格点，则称为格点多边形．记格点多边形的面积为S，其内部的格点数记为n，边界上的格点数记为l，例如图中△ABC是格点三角形，对应的S=1，n=0，l=4．