题目内容
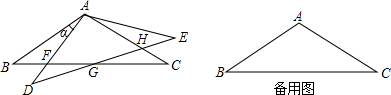
15. 如图,正方形ABCD中,AB=1,点E、F分别是边BC、CD上的两点,∠EAF=45°,AG⊥EF于点G,连接BD分别交AE、AF于点M、N,将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH.以下结论正确的是①②④.
如图,正方形ABCD中,AB=1,点E、F分别是边BC、CD上的两点,∠EAF=45°,AG⊥EF于点G,连接BD分别交AE、AF于点M、N,将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH.以下结论正确的是①②④.①AG=1;②△CEF的周长是定值,定值是2;③DF2+BE2=EF2;④DN2+BM2=MN2.
分析 由正方形的性质得AB=AD=1,∠BAC=∠ADC=∠ABC=90°,于是可把△ADF绕点A顺时针旋转90°可得到△ABP,如图,根据旋转得性质得AP=AF,BP=DF,∠ABP=∠ADC=90°,∠PAF=∠BAD=90°,易得点P在CB的延长线上,再证明△AEP≌△AEF得到EP=EF,根据全等三角形的对应边上的高相等得到AG=AB=1,可对①进行判断;所以EF=EP=BE+BP=BE+DF,则可对③进行判断;同时可计算出△CEF的周长=2,则可对②进行判断;连结NH,如图,根据正方形的性质得∠ABD=∠ADB=45°,再根据旋转的性质得AM=AH,BM=DH,∠ADH=∠ABM=45°,∠MAH=90°,由于∠MAN=45°,则∠NAH=45°,可计算出∠NDH=90°,根据勾股定理得DN2+DH2=NH2,则DN2+BM2=NH2,然后证明△ANM≌△ANH得到MN=NH,则可对④进行判断.
解答 解:∵四边形ABCD为正方形,
∴AB=AD=1,∠BAC=∠ADC=∠ABC=90°,
∴把△ADF绕点A顺时针旋转90°可得到△ABP,如图,
∴AP=AF,BP=DF,∠ABP=∠ADC=90°,∠PAF=∠BAD=90°,
∴∠ABP+∠ABC=180°,即点P在CB的延长线上,
∵∠EAF=45°,
∴∠PAE=45°,
在△AEP和△AEF中
$\left\{\begin{array}{l}{AE=AE}\\{∠PAE=∠EAF}\\{AP=AF}\end{array}\right.$,
∴△AEP≌△AEF,
∴EP=EF,
∵AG⊥EF,AB⊥EP,
∴AG=AB=1,所以①正确;
∵EF=EP=BE+BP=BE+DF,所以③错误;
∴△CEF的周长=EF+CE+CF=BE+EC+CF+DF=CB+CD=1+1=2,所以②正确;
连结NH,如图,
∵四边形ABCD为正方形,
∴∠ABD=∠ADB=45°,
∵△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH,
∴AM=AH,BM=DH,∠ADH=∠ABM=45°,∠MAH=90°,
∵∠MAN=45°,
∴∠NAH=45°,
∴∠NDH=45°+45°=90°,
∴DN2+DH2=NH2,
∴DN2+BM2=NH2,
在△ANM和△ANH中
$\left\{\begin{array}{l}{AN=AN}\\{∠MAN=∠HAN}\\{AM=AH}\end{array}\right.$,
∴△ANM≌△ANH,
∴MN=NH,
∴DN2+BM2=MN2,所以④正确.
故答案为①②④.
点评 本题考查了本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了全等三角形的判定与性质和正方形的性质.

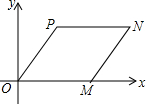 如图所示,在平行直角坐标系中,?OMNP的顶点P坐标是(3,4),顶点M坐标是(4,0)、则顶点N的坐标是( )
如图所示,在平行直角坐标系中,?OMNP的顶点P坐标是(3,4),顶点M坐标是(4,0)、则顶点N的坐标是( )| A. | N(7,4) | B. | N(8,4) | C. | N(7,3) | D. | N(8,3) |
| A. | 1.0×10-8m | B. | 1.0×10-9m | C. | 1.0×10-10m | D. | 1.0×109m |
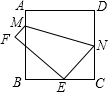 如图所示,将边长为6cm的正方形纸片ABCD折叠,使点D落在BC中点E处,点A落在F处,折痕为MN,则线段CN的长是( )
如图所示,将边长为6cm的正方形纸片ABCD折叠,使点D落在BC中点E处,点A落在F处,折痕为MN,则线段CN的长是( )| A. | 2.25 | B. | 3 | C. | 4 | D. | 4.5 |