题目内容
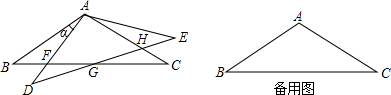
20.如图,△ABC中,AB=AC=2,∠B=30°,将△ABC绕顶点A逆时针旋转得到△ADE.设旋转角度为α度(0°<α<120°),AD交BC于点F,DE分别交BC、AC于点G、H.试探究以下问题:(1)当α=60°或90°时,△ABF为直角三角形;
(2)当BF=2或$\frac{2\sqrt{3}}{3}$时,△ABF为等腰三角形;
(3)当△ADH为等腰三角形时,求BF的值;
(4)连接BD,是否存在角α,使得四边形ABDH为平行四边形?如果存在,直接写出α的大小;如果不存在,请说明理由.
分析 (1)分两种情况:①当∠AFB=90°时;由角的互余关系即可求出结果;②当∠BAF=90°时,即α=90°;
(2)分两种情况:①当BF=AB时,BF=AB=2;②当BF=AF时,α=∠B=30°,作FM⊥AB于M,由等腰三角形的性质得出BM=$\frac{1}{2}$AB=1,由三角函数求出BF即可;
(3)分两种情况:①当AD=DH时;作FN⊥AB于N,设FN=x,则BF=2x,BN=$\sqrt{3}$x,AN=FN=x,根据题意得出方程,解方程即可得出结果;
②当AH=DH时,∠DAH=∠D=30°,由三角函数即可求出BF;
(4)若四边形ABDH为平行四边形,则AB∥DH,得出α=∠D=30°,由等腰三角形的性质得出∠ADB≠∠DAH,得出BD与AH不平行,即可得出结论.
解答 解:(1)分两种情况:
①当∠AFB=90°时,α=90°-∠B=60°;
②当∠BAF=90°时,即α=90°;
∴当α=60°或90°时,△ABF为直角三角形;
故答案为:60°或90°;
(2)分两种情况:①当BF=AB时,BF=AB=2;
②当BF=AF时,α=∠B=30°,
作FM⊥AB于M,如图1所示: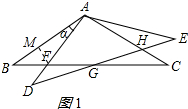 则BM=$\frac{1}{2}$AB=1,
则BM=$\frac{1}{2}$AB=1,
∵cos∠B=$\frac{BM}{BF}$,
∴BF=$\frac{BM}{cos30°}$=$\frac{1}{\frac{\sqrt{3}}{2}}$=$\frac{2\sqrt{3}}{3}$,
综上所述,当BF=2或$\frac{2\sqrt{3}}{3}$时,△ABF为等腰三角形;
故答案为:2或$\frac{2\sqrt{3}}{3}$;
(3)分两种情况:
①当AD=DH时,∠DAC=∠AHD=$\frac{1}{2}$(180°-30°)=75°,
∴∠BAD=45°,
作FN⊥AB于N,如图2所示: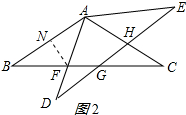
设FN=x,则BF=2x,BN=$\sqrt{3}$x,AN=FN=x,
则$\sqrt{3}$x+x=2,
解得:x=$\sqrt{3}$-1,
∴BF=2$\sqrt{3}$-2;
②当AH=DH时,∠DAH=∠D=30°,
∴∠BAF=120°-30°=90°,
∵cos∠B=$\frac{AB}{BF}$,
∴BF=$\frac{AB}{cos30°}$=$\frac{2}{\frac{\sqrt{3}}{2}}$=$\frac{4\sqrt{3}}{3}$;
综上所述:当△ADH为等腰三角形时,BF的值为2$\sqrt{3}$-2或$\frac{4\sqrt{3}}{3}$;
(4)不存在,理由如下:
若四边形ABDH为平行四边形,
则AB∥DH,
∴α=∠D=30°,
∵AB=AD,
∴∠ADB=∠ABD=75°,
∵AB=AC=2,∠B=30°,
∴∠BAC=120°,
∴∠DAH=90°,∠ADB≠∠DAH,
∴BD与AH不平行,
∴四边形ABDH不是平行四边形;
∴不存在角α,使得四边形ABDH为平行四边形.
点评 本题是几何变换综合题目,考查了旋转的性质、等腰三角形的性质、三角函数、等腰直角三角形的性质、平行四边形的判定与性质等知识;本题综合性强,难度较大,需要进行分类讨论才能得出结果.

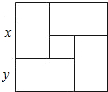 用四个完全一样的长方形和一个小正方形拼成如图所示的大长方形的长和宽,已知大正方形的面积是121,小正方形的面积是9,若用x,y(x>y)表示长方形的长和宽,则下列关系中不正确的是( )
用四个完全一样的长方形和一个小正方形拼成如图所示的大长方形的长和宽,已知大正方形的面积是121,小正方形的面积是9,若用x,y(x>y)表示长方形的长和宽,则下列关系中不正确的是( )| A. | x+y=11 | B. | x2+y2=180 | C. | x-y=3 | D. | x•y=28 |
 在某项针对18-35岁的青年人每天发微信数量的调查中,设一个人的“日均发微信条数”为m,当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微信条数”的调查,根据调查数据整理并制作图表如下:
在某项针对18-35岁的青年人每天发微信数量的调查中,设一个人的“日均发微信条数”为m,当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微信条数”的调查,根据调查数据整理并制作图表如下:青年人日均发微信条数统计表
| m | 频数 | 百分数 |
| A级(0≤m<5) | 90 | 0.3 |
| B级(5≤m<10) | 120 | 0.4 |
| C级(10≤m<15) | b | 0.2 |
| D级(15≤m<20) | 30 | a |
(1)在表中:a=0.1,b=60;
(2)补全频数分布直方图;
(3)若北京市常住人口中18~35岁的青年人大约有530万人,试估计其中“日均发微信条数”不少于10条的大约有多少万人.
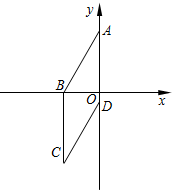 如图,四边形ABCD为菱形,已知A(0,4),B(-3,0),点D在y轴上.求点D的坐标和对角线AC的长.
如图,四边形ABCD为菱形,已知A(0,4),B(-3,0),点D在y轴上.求点D的坐标和对角线AC的长.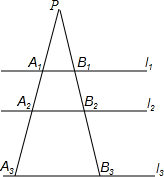 如图,l1∥l2∥l3,B1B2=$\frac{1}{2}$B2B3,又A1B1=1,A3B3=3,则A2B2=$\frac{5}{3}$,$\frac{P{A}_{1}}{{A}_{1}{A}_{2}}$=$\frac{3}{2}$.
如图,l1∥l2∥l3,B1B2=$\frac{1}{2}$B2B3,又A1B1=1,A3B3=3,则A2B2=$\frac{5}{3}$,$\frac{P{A}_{1}}{{A}_{1}{A}_{2}}$=$\frac{3}{2}$.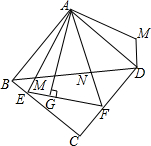 如图,正方形ABCD中,AB=1,点E、F分别是边BC、CD上的两点,∠EAF=45°,AG⊥EF于点G,连接BD分别交AE、AF于点M、N,将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH.以下结论正确的是①②④.
如图,正方形ABCD中,AB=1,点E、F分别是边BC、CD上的两点,∠EAF=45°,AG⊥EF于点G,连接BD分别交AE、AF于点M、N,将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH.以下结论正确的是①②④.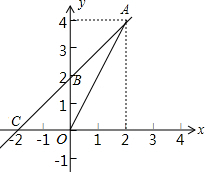 如图,一次函数y=kx+b的图象经过(2,4)、(0,2)两点,与x轴相交于点C.求:
如图,一次函数y=kx+b的图象经过(2,4)、(0,2)两点,与x轴相交于点C.求: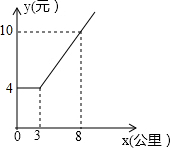 某市出租车公司收费标准如图所示,
某市出租车公司收费标准如图所示,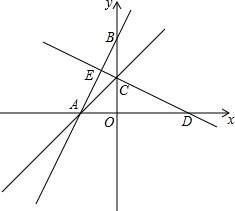 如图,在平面直角坐标系中,直线y=2x+4交x轴于点A,交Y轴于点B,点C为BO中点.
如图,在平面直角坐标系中,直线y=2x+4交x轴于点A,交Y轴于点B,点C为BO中点.