题目内容
6. 如图,甲、乙两人分别从A(1,$\sqrt{3}$),B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向,乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点.
如图,甲、乙两人分别从A(1,$\sqrt{3}$),B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向,乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点.(1)请说明甲、乙两人到达O点前,MN与AB不可能平行;
(2)当t为何值时,△OMN∽△OBA;
(3)甲、乙两人之间的距离为MN的长,设s=MN2,直接写出s与t之间的函数关系式.
分析 (1)判断出甲、乙两人到达O点前,只有当t=0时,△OMN∽△OAB,即可推得MN与AB不可能平行.
(2)根据题意,分三种情况:①t<$\frac{1}{2}$时;②当$\frac{1}{2}$<t<$\frac{3}{2}$时;③当t>$\frac{3}{2}$时;求出当t为何值时,△OMN∽△OBA.
(3)根据题意,分三种情况:①t≤$\frac{1}{2}$时;②当$\frac{1}{2}$<t≤$\frac{3}{2}$时;③当t>$\frac{3}{2}$时;写出s与t之间的函数关系式即可.
解答 解:(1)∵A点的坐标为(1,$\sqrt{3}$),
∴OA=$\sqrt{{1}^{2}{+(\sqrt{3})}^{2}}$=2;
∵OM=2-4t,ON=6-4t,
∴当$\frac{2-4t}{2}$=$\frac{6-4t}{6}$时,解得t=0,
∴甲、乙两人到达O点前,只有当t=0时,△OMN∽△OAB,
∴MN与AB不可能平行.
(2)∵甲到达O点的时间为t=$\frac{1}{2}$,乙到达O点的时间为t=$\frac{6}{4}$=$\frac{3}{2}$,
∴甲先到达O点,
∴t=$\frac{1}{2}$或t=$\frac{3}{2}$时,O、M、N三点不能连接成三角形.
①t<$\frac{1}{2}$时,
如果△OMN∽△OBA,则有$\frac{2-4t}{6}$=$\frac{6-4t}{2}$,
解得t=2>$\frac{1}{2}$,
∴△OMN不可能和△OBA相似.
②当$\frac{1}{2}$<t<$\frac{3}{2}$时,
∠MON>∠AOB,
显然△OMN不可能和△OBA相似.
③当t>$\frac{3}{2}$时,
$\frac{4t-2}{6}$=$\frac{4t-6}{2}$,
解得t=2>$\frac{3}{2}$,
∴当t=2时,△OMN∽△OBA.
(3)①当t≤$\frac{1}{2}$时,如图1,过点M作MH⊥x轴于点H,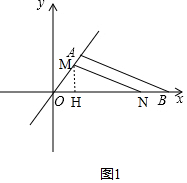 ,
,
在Rt△MOH中,
∵∠AOB=60°,
∴MH=OMsin60°=(2-4t)×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$(1-2t),
∴OH=OMcos60°=(2-4t)×$\frac{1}{2}$=1-2t,
∴NH=(6-4t)-(1-2t)=5-2t,
∴s=[$\sqrt{3}$(1-2t)]2+(5-2t)2
=3(4t2-4t+1)+(4t2-20t+25)
=16t2-32t+28.
②当$\frac{1}{2}$<t≤$\frac{3}{2}$时,如图2,作MH⊥x轴于点H,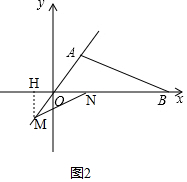 ,
,
在Rt△MOH中,
MH=$\frac{\sqrt{3}}{2}$(4t-2)=$\sqrt{3}$(2t-1),
NH=$\frac{1}{2}$(4t-2)+(6-4t)=5-2t,
∴s=[$\sqrt{3}$(1-2t)]2+(5-2t)2=16t2-32t+28.
③当t>$\frac{3}{2}$时,同理可得s=[$\sqrt{3}$(1-2t)]2+(5-2t)2=16t2-32t+28.
综上,可得s=[$\sqrt{3}$(1-2t)]2+(5-2t)2=16t2-32t+28.
点评 此题主要考查了三角形相似的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案 如图,扇形OAB的圆心角为90°,点C,D是弧AB的三等分点,半径OC,OD分别与弦AB交于点E,F,下列说法错误的是( )
如图,扇形OAB的圆心角为90°,点C,D是弧AB的三等分点,半径OC,OD分别与弦AB交于点E,F,下列说法错误的是( )| A. | AE=EF=FB | B. | AC=CD=DB | C. | EC=FD | D. | ∠DFB=75° |
 如图,某物体在20秒内的速度与时间的关系图,物体最高速度为20厘米/秒.
如图,某物体在20秒内的速度与时间的关系图,物体最高速度为20厘米/秒.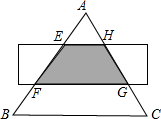 如图,△ABC是面积为18cm2的等边三角形,被一长边平行于BC的矩形所截,AB被截成三等份,则图中阴影部分的面积为6 cm2.
如图,△ABC是面积为18cm2的等边三角形,被一长边平行于BC的矩形所截,AB被截成三等份,则图中阴影部分的面积为6 cm2.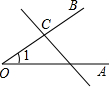
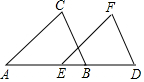 如图,∠C=∠F,AC∥EF,AE=BD,求证:①△ABC≌EDF;②BC∥DF.
如图,∠C=∠F,AC∥EF,AE=BD,求证:①△ABC≌EDF;②BC∥DF.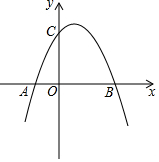 如图,已知抛物线y=-x2+4x+5与x轴的两个交点为A、B,与y轴交于点C.
如图,已知抛物线y=-x2+4x+5与x轴的两个交点为A、B,与y轴交于点C.