题目内容
16.解方程(1)9x2-1=3x+1
(2)2x2+x=2(1-x)
分析 (1)首先去括号,进而合并同类项,再利用因式分解法解方程得出答案;
(2)直接利用十字相乘法解方程得出答案.
解答 解:(1)9x2-1=3x+1
(3x+1)(3x-1)-(3x+1)=0,
(3x+1)(3x-2)=0,
解得:x1=-$\frac{1}{3}$,x2=$\frac{2}{3}$;
(2)2x2+x=2(1-x)
2x2+x+2x-2=0,
2x2+3x-2=0,
(2x+1)(x-2)=0,
解得:x1=-$\frac{1}{2}$,x2=2.
点评 此题主要考查了因式分解法解方程,正确因式分解是解题关键.

练习册系列答案
相关题目
7.若二次根式$\sqrt{x-2}$有意义,则 x 的取值范围为( )
| A. | x>2 | B. | x<2 | C. | x≤2 | D. | x≥2 |
8.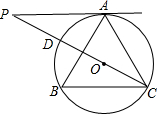 如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点P,CP交⊙O于点D,若AC=3,则△APC的面积为( )
如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点P,CP交⊙O于点D,若AC=3,则△APC的面积为( )
 如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点P,CP交⊙O于点D,若AC=3,则△APC的面积为( )
如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点P,CP交⊙O于点D,若AC=3,则△APC的面积为( )| A. | 3$\sqrt{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{2}$$\sqrt{3}$ | D. | $\frac{9}{4}$$\sqrt{3}$ |
1.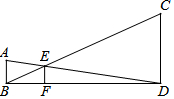 如图,AB、CD、EF都与BD垂直,且AB=1,CD=3,那么EF的长是( )
如图,AB、CD、EF都与BD垂直,且AB=1,CD=3,那么EF的长是( )
 如图,AB、CD、EF都与BD垂直,且AB=1,CD=3,那么EF的长是( )
如图,AB、CD、EF都与BD垂直,且AB=1,CD=3,那么EF的长是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
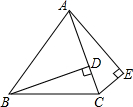 如图,在△ABC中,AC=BC,BD⊥AC于点D,在△ABC外作∠CAE=∠CBD,过点C作CE⊥AE于点E.如果∠BCE=140°,求∠BAC的度数.
如图,在△ABC中,AC=BC,BD⊥AC于点D,在△ABC外作∠CAE=∠CBD,过点C作CE⊥AE于点E.如果∠BCE=140°,求∠BAC的度数. 如图,甲、乙两人分别从A(1,$\sqrt{3}$),B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向,乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点.
如图,甲、乙两人分别从A(1,$\sqrt{3}$),B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向,乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点.