题目内容
 如图,点O是?ABCD的对角线交点,AC=38mm,BD=24mm,AD=14mm,那么△OBC的周长等于( )
如图,点O是?ABCD的对角线交点,AC=38mm,BD=24mm,AD=14mm,那么△OBC的周长等于( )| A、40mm | B、44mm |
| C、45mm | D、50mm |
考点:平行四边形的性质
专题:
分析:根据平行四边形的对边相等,对角线互相平分两条性质求BC,OB,OC的长,可求△OBC的周长.
解答:解:由平行四边形的对边相等,得BC=AD=14mm,
由平行四边形中对角线相互平分,得
OB=
BD,OC=
AC,
∴△OBC的周长=OB+OC+BC
=
(AC+BD)+BC
=31+14
=45mm.
故选C.
由平行四边形中对角线相互平分,得
OB=
| 1 |
| 2 |
| 1 |
| 2 |
∴△OBC的周长=OB+OC+BC
=
| 1 |
| 2 |
=31+14
=45mm.
故选C.
点评:本题主要考查了平行四边形的基本性质,并利用性质解题.平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
已知反比例函数y=
的图象经过点P(2,-3),则k的值为( )
| k |
| x |
| A、-6 | ||
| B、5 | ||
C、
| ||
| D、2 |
如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并观察,在第n个图中,共有瓷砖( )块.


| A、n2+n+6 |
| B、n2+4n+6 |
| C、n2+5n+6 |
| D、n2+5n+5 |
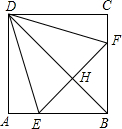 如图,正方形ABCD中,点E,F分别在AB,BC边上,且△DEF是等边三角形,连接BD交EF于H,则∠FDH的度数为( )
如图,正方形ABCD中,点E,F分别在AB,BC边上,且△DEF是等边三角形,连接BD交EF于H,则∠FDH的度数为( )| A、15° | B、20° |
| C、25° | D、30° |
二次函数y=(x-3)2+1的最小值是( )
| A、1 | B、-1 | C、3 | D、-3 |
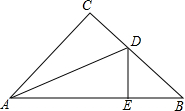 如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB于E,若AC=m,CD=n,则△BDE的周长为( )
如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB于E,若AC=m,CD=n,则△BDE的周长为( )| A、m+n | B、m-n |
| C、2m+n | D、2n+m |
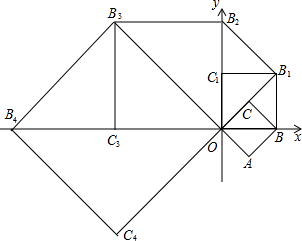 如图,在平面直角坐标系xOy中,有一边长为1的正方形OABC,点B在x轴的正半轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则B2的坐标是
如图,在平面直角坐标系xOy中,有一边长为1的正方形OABC,点B在x轴的正半轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则B2的坐标是