题目内容
设直线y=kx+k-1和直线y=(k+1)x+k(k为正整数)与x轴所围成的图形的面积为SK(k=1,2,3,…,8),那么S1+S2+…+S8的值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:一次函数图象上点的坐标特征
专题:规律型
分析:当k=1时,求出直线y=x,y=2x+1与x轴的交点坐标分别为(0,0),(-
,0),再求出它们的交点坐标为(-1,-1),然后根据三角形面积公式得到S1=
×
;利用同样的方法得到S2=
(
-
),S3=
(
-
),S8=
(
-
),最后把它们相加即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 8 |
| 9 |
| 7 |
| 8 |
解答:解:当k=1时,两直线解析式为y=x,y=2x+1,两直线与x轴的交点坐标分别为(0,0),(-
,0),解方程组
得
,即两直线的交点坐标为(-1,-1),所以S1=
×(0+
)×1=
×
;
当k=2时,两直线解析式为y=2x+1,y=3x+2,两直线与x轴的交点坐标分别为(-
,0),(-
,0),解方程组
得
,即两直线的交点坐标为(-1,-1),所以S2=
×(-
+
)×1=
(
-
),
同样可得S3=
(
-
),S8=
(
-
),
所以S1+S2+…+S8=
×
+
(
-
)+
(
-
)+…+
(
-
)=
(
+
-
+
-
+…+
-
)=
×
=
.
故选A.
| 1 |
| 2 |
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当k=2时,两直线解析式为y=2x+1,y=3x+2,两直线与x轴的交点坐标分别为(-
| 1 |
| 2 |
| 2 |
| 3 |
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
同样可得S3=
| 1 |
| 2 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 8 |
| 9 |
| 7 |
| 8 |
所以S1+S2+…+S8=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 8 |
| 9 |
| 7 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 2 |
| 3 |
| 8 |
| 9 |
| 7 |
| 8 |
| 1 |
| 2 |
| 8 |
| 9 |
| 4 |
| 9 |
故选A.
点评:本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-bk,0);与y轴的交点坐标是(0,b);直线上任意一点的坐标都满足函数关系式y=kx+b.也考查了规律型问题的解决方法.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
 如图,点O是?ABCD的对角线交点,AC=38mm,BD=24mm,AD=14mm,那么△OBC的周长等于( )
如图,点O是?ABCD的对角线交点,AC=38mm,BD=24mm,AD=14mm,那么△OBC的周长等于( )| A、40mm | B、44mm |
| C、45mm | D、50mm |
以下列各组数为边长的三角形是直角三角形的是( )
| A、1、2、3 | ||
| B、5、12、13 | ||
C、1、1、
| ||
| D、6、7、8 |
在Rt△ABC中,∠C=90°,AC=6,AB=10,则BC的值为( )
| A、6 | ||
| B、8 | ||
| C、10 | ||
D、2
|
二次函数y=x2-2x+2的图象与x轴的交点个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
若点A(1,y1)、B(2,y2)都在反比例函数y=
的图象上,则y1,y2的大小关系为( )
| 6 |
| x |
| A、y1≥y2 |
| B、y1>y2 |
| C、y1<y2 |
| D、y1≤y2 |
下列图形中,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
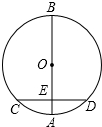 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为