题目内容
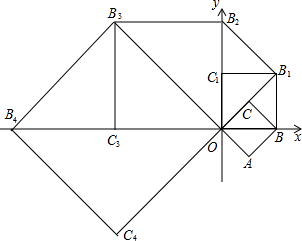 如图,在平面直角坐标系xOy中,有一边长为1的正方形OABC,点B在x轴的正半轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则B2的坐标是
如图,在平面直角坐标系xOy中,有一边长为1的正方形OABC,点B在x轴的正半轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则B2的坐标是考点:正方形的性质,坐标与图形性质
专题:规律型
分析:根据已知条件和勾股定理求出OB2的长度即可求出B2的坐标,再根据题意和图形可看出每经过一次变化,都顺时针旋转45°,边长都乘以
,所以可求出从B到B2014的后变化的坐标.
| 2 |
解答:解:∵四边形OABC是正方形,OB=1,
∴OB1=
=2,
∴OB2=
=2
,
∴B2的坐标是(0,2
),
根据题意和图形可看出每经过一次变化,都顺时针旋转45°,边长都乘以
,
∴旋转8次则OB旋转一周,
∵从B到B2014经过了2014次变化,
2014÷8=251…6,
∴从B到B2014与B6都在y负半轴上,
∴点B2014的坐标是(0,-
2005).
故答案为:(0,2
),(0,-
2005).
∴OB1=
(
|
∴OB2=
| OB12+B12B22 |
| 2 |
∴B2的坐标是(0,2
| 2 |
根据题意和图形可看出每经过一次变化,都顺时针旋转45°,边长都乘以
| 2 |
∴旋转8次则OB旋转一周,
∵从B到B2014经过了2014次变化,
2014÷8=251…6,
∴从B到B2014与B6都在y负半轴上,
∴点B2014的坐标是(0,-
| 2 |
故答案为:(0,2
| 2 |
| 2 |
点评:本题主要考查正方形的性质和坐标与图形的性质的知识点,解答本题的关键是由点坐标的规律发现每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变为原来的
倍,此题难度较大.
| 2 |

练习册系列答案
相关题目
下列各数中,最大的是( )
| A、2 | B、0 | C、1 | D、-3 |
4的平方根是( )
| A、2 | B、-2 | C、±2 | D、16 |
 如图,点O是?ABCD的对角线交点,AC=38mm,BD=24mm,AD=14mm,那么△OBC的周长等于( )
如图,点O是?ABCD的对角线交点,AC=38mm,BD=24mm,AD=14mm,那么△OBC的周长等于( )| A、40mm | B、44mm |
| C、45mm | D、50mm |
若点A(1,y1)、B(2,y2)都在反比例函数y=
的图象上,则y1,y2的大小关系为( )
| 6 |
| x |
| A、y1≥y2 |
| B、y1>y2 |
| C、y1<y2 |
| D、y1≤y2 |
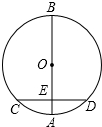 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为 如图,四边形ABCD是菱形,AC、BD交于点O,DH⊥AB于H,连OH,若AC=8,OH=3,则AH=
如图,四边形ABCD是菱形,AC、BD交于点O,DH⊥AB于H,连OH,若AC=8,OH=3,则AH=