题目内容
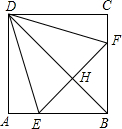 如图,正方形ABCD中,点E,F分别在AB,BC边上,且△DEF是等边三角形,连接BD交EF于H,则∠FDH的度数为( )
如图,正方形ABCD中,点E,F分别在AB,BC边上,且△DEF是等边三角形,连接BD交EF于H,则∠FDH的度数为( )| A、15° | B、20° |
| C、25° | D、30° |
考点:正方形的性质,全等三角形的判定与性质,等边三角形的性质
专题:
分析:根据正方形的性质可得AD=CD,∠A=∠C=90°,根据等边三角形的性质可得DE=DF,然后利用“HL”证明Rt△ADE和Rt△CDF全等,根据全等三角形对应角相等可得∠ADE=∠CDF,然后求出∠EDH=∠FDH,再根据等边三角形的每一个角都是60°计算即可得解.
解答:解:在正方形ABCD中,AD=CD,∠A=∠C=90°,
在△DEF是等边三角形,DE=DF,
在Rt△ADE和Rt△CDF中,
,
所以,Rt△ADE≌Rt△CDF(HL),
所以,∠ADE=∠CDF,
所以,∠EDH=∠FDH=
∠EDF=
×60°=30°.
故选D.
在△DEF是等边三角形,DE=DF,
在Rt△ADE和Rt△CDF中,
|
所以,Rt△ADE≌Rt△CDF(HL),
所以,∠ADE=∠CDF,
所以,∠EDH=∠FDH=
| 1 |
| 2 |
| 1 |
| 2 |
故选D.
点评:本题考查了正方形的性质,等边三角形的性质,全等三角形的判定与性质,熟记各性质并求出三角形全等是解题的关键.

练习册系列答案
相关题目
下列各数中,最大的是( )
| A、2 | B、0 | C、1 | D、-3 |
在数轴上,与表示-1的点距离为3的点所表示的数是( )
| A、-2或-4 | B、2或-4 |
| C、2或4 | D、-2或4 |
 如图,点O是?ABCD的对角线交点,AC=38mm,BD=24mm,AD=14mm,那么△OBC的周长等于( )
如图,点O是?ABCD的对角线交点,AC=38mm,BD=24mm,AD=14mm,那么△OBC的周长等于( )| A、40mm | B、44mm |
| C、45mm | D、50mm |
下列问题最适合采用全面调查的是( )
| A、了解某地区七年级学生的体重情况 |
| B、我市选拔跳远成绩最好的男同学参加市运动会 |
| C、调查某种食品是否符合国家安全标准 |
| D、了解某市市民日常出行所使用的交通工具 |
以下列各组数为边长的三角形是直角三角形的是( )
| A、1、2、3 | ||
| B、5、12、13 | ||
C、1、1、
| ||
| D、6、7、8 |
二次函数y=x2-2x+2的图象与x轴的交点个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |