题目内容
二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)中的x与y的部分对应值如下表:
(1)ac<0;
(2)当x>1时,y的值随x值得增大而增大;
(3)-1是方程ax2+bx+c=0的一个根;
(4)当-1<x<2时,ax2+bx+c<0
其中正确的个数为( )
| x | … | 0 | 1 | 2 | … |
| y | … | -4 | -4 | 0 | … |
(2)当x>1时,y的值随x值得增大而增大;
(3)-1是方程ax2+bx+c=0的一个根;
(4)当-1<x<2时,ax2+bx+c<0
其中正确的个数为( )
| A、4个 | B、3个 | C、2个 | D、1个 |
考点:二次函数的性质
专题:
分析:根据条件可求出二次函数解析式,再进行判定即可.
解答:解:
由条件可知x=0时,y=-4,x=1时,y=-4,x=2时,y=0,
可得方程组
,解得
,
∴二次函数解析式为y=2x2-2x-4,
∴ac<0,
∴(1)正确;
其对称轴为x=1,且开口向上,
∴当x>1时,y的值随x值得增大而增大,
∴(2)正确;
当x=-1时,y=2×(-1)2-2(-1)-4=0,
∴-1是方程ax2+bx+c=0的一个根,
∴(3)正确;
令y=0得2x2-2x-4=0,解得x=-1或x=2,且开口向上,
∴当-1<x<2时,2x2-2x-4<0,
∴(4)正确;
综上可知正确的有四个,
故选A.
由条件可知x=0时,y=-4,x=1时,y=-4,x=2时,y=0,
可得方程组
|
|
∴二次函数解析式为y=2x2-2x-4,
∴ac<0,
∴(1)正确;
其对称轴为x=1,且开口向上,
∴当x>1时,y的值随x值得增大而增大,
∴(2)正确;
当x=-1时,y=2×(-1)2-2(-1)-4=0,
∴-1是方程ax2+bx+c=0的一个根,
∴(3)正确;
令y=0得2x2-2x-4=0,解得x=-1或x=2,且开口向上,
∴当-1<x<2时,2x2-2x-4<0,
∴(4)正确;
综上可知正确的有四个,
故选A.
点评:本题主要考查待定系数法求二次函数解析式,利用待定系数法求出二次函数的解析式是解题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 函数y=x2+bx+c与y=x的图象如图所示,有以上结论:
函数y=x2+bx+c与y=x的图象如图所示,有以上结论: 如图,AD∥BC,DC⊥AD,AE平分∠BAD,且点E是DC的中点.
如图,AD∥BC,DC⊥AD,AE平分∠BAD,且点E是DC的中点.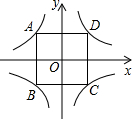 在同一平面直角坐标系中,反比例函数y=
在同一平面直角坐标系中,反比例函数y=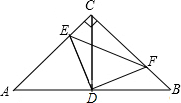 如图,在等腰直角三角形ABC中,∠C=90°,AC=BC=4,点D是AB的中点,E、F在射线AC与射线CB上运动,且满足AE=CF;当点E运动到与点C的距离为1时,则△DEF的面积=
如图,在等腰直角三角形ABC中,∠C=90°,AC=BC=4,点D是AB的中点,E、F在射线AC与射线CB上运动,且满足AE=CF;当点E运动到与点C的距离为1时,则△DEF的面积=