题目内容
已知|a-1|+|ab-2|=0,求代数式
+
+
+…+
的值.
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+2014)(b+2014) |
考点:代数式求值,非负数的性质:绝对值
专题:
分析:根据非负数的性质得到a=1,ab=2.易求b=2;然后将所求的代数式中的分式一项拆为两项,找到规律进行计算即可.
解答:解:∵|a-1|+|ab-2|=0,
∴a=1,ab=2.
∴b=2,
∴
+
+
+…+
=
+
+…+
=1-
+
-
+…+
-
=1-
=
.
∴a=1,ab=2.
∴b=2,
∴
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+2014)(b+2014) |
=
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 2015×2016 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2015 |
| 1 |
| 2016 |
=1-
| 1 |
| 2016 |
=
| 2015 |
| 2016 |
点评:本题考查了代数式求值和非负数的性质.找到规律是解题的难点.

练习册系列答案
相关题目
二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)中的x与y的部分对应值如下表:
(1)ac<0;
(2)当x>1时,y的值随x值得增大而增大;
(3)-1是方程ax2+bx+c=0的一个根;
(4)当-1<x<2时,ax2+bx+c<0
其中正确的个数为( )
| x | … | 0 | 1 | 2 | … |
| y | … | -4 | -4 | 0 | … |
(2)当x>1时,y的值随x值得增大而增大;
(3)-1是方程ax2+bx+c=0的一个根;
(4)当-1<x<2时,ax2+bx+c<0
其中正确的个数为( )
| A、4个 | B、3个 | C、2个 | D、1个 |
如果ab=-1,n=2012,那么an•bn的值为( )
| A、-2012 | B、2012 |
| C、1 | D、-1 |
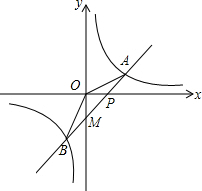 如图,一次函数y=kx-1的图象和反比例函数y=
如图,一次函数y=kx-1的图象和反比例函数y=