题目内容
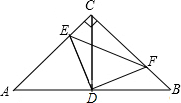 如图,在等腰直角三角形ABC中,∠C=90°,AC=BC=4,点D是AB的中点,E、F在射线AC与射线CB上运动,且满足AE=CF;当点E运动到与点C的距离为1时,则△DEF的面积=
如图,在等腰直角三角形ABC中,∠C=90°,AC=BC=4,点D是AB的中点,E、F在射线AC与射线CB上运动,且满足AE=CF;当点E运动到与点C的距离为1时,则△DEF的面积=考点:全等三角形的判定与性质
专题:动点型
分析:易证△ADE≌△CDF,△CDE≌△BCF,可得四边形CEDF面积是△ABC面积的一半,再计算△CEF的面积即可解题.
解答:解:①E在线段AC上,
∵在△ADE和△CDF中,
,
∴△ADE≌△CDF,(SAS),
∴同理△CDE≌△BDF,
∴四边形CEDF面积是△ABC面积的一半,
∵CE=1,∴CF=4-1=3,
∴△CEF的面积=
CE•CF=
,
∴△DEF的面积=
×2
×2
-
=
.
②E'在AC延长线上,
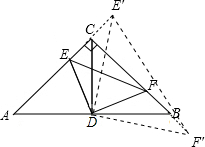
∵AE'=CF',AC=BC=4,∠ACB=90°,
∴CE'=BF',∠ACD=∠CBD=45°,CD=AD=BD=2
,
∴∠DCE'=∠DBF'=135°,
∵在△CDE'和△BDF'中,
,
∴△CDE'≌△BDF',(SAS)
∴DE'=DF',∠CDE'=∠BDF',
∵∠CDE'+∠BDE'=90°,
∴∠BDE'+∠BDF'=90°,即∠E'DF'=90°,
∵DE'2=CE'2+CD2-2CD•CE'cos135°=1+8+2×2
×
=13,
∴S△E'DF'=
DE'2=
.
故答案为
或
.
∵在△ADE和△CDF中,
|
∴△ADE≌△CDF,(SAS),
∴同理△CDE≌△BDF,
∴四边形CEDF面积是△ABC面积的一半,
∵CE=1,∴CF=4-1=3,
∴△CEF的面积=
| 1 |
| 2 |
| 3 |
| 2 |
∴△DEF的面积=
| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
②E'在AC延长线上,

∵AE'=CF',AC=BC=4,∠ACB=90°,
∴CE'=BF',∠ACD=∠CBD=45°,CD=AD=BD=2
| 2 |
∴∠DCE'=∠DBF'=135°,
∵在△CDE'和△BDF'中,
|
∴△CDE'≌△BDF',(SAS)
∴DE'=DF',∠CDE'=∠BDF',
∵∠CDE'+∠BDE'=90°,
∴∠BDE'+∠BDF'=90°,即∠E'DF'=90°,
∵DE'2=CE'2+CD2-2CD•CE'cos135°=1+8+2×2
| 2 |
| ||
| 2 |
∴S△E'DF'=
| 1 |
| 2 |
| 13 |
| 2 |
故答案为
| 13 |
| 2 |
| 5 |
| 2 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ADE≌△CDF和△CDE≌△BCF是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)中的x与y的部分对应值如下表:
(1)ac<0;
(2)当x>1时,y的值随x值得增大而增大;
(3)-1是方程ax2+bx+c=0的一个根;
(4)当-1<x<2时,ax2+bx+c<0
其中正确的个数为( )
| x | … | 0 | 1 | 2 | … |
| y | … | -4 | -4 | 0 | … |
(2)当x>1时,y的值随x值得增大而增大;
(3)-1是方程ax2+bx+c=0的一个根;
(4)当-1<x<2时,ax2+bx+c<0
其中正确的个数为( )
| A、4个 | B、3个 | C、2个 | D、1个 |
下列结论正确的是( )
| A、a一定是正数 |
| B、倒数等于它本身的数只有1 |
| C、面积为2的正方形的边长a是无理数 |
| D、0是最小的整数 |
如果ab=-1,n=2012,那么an•bn的值为( )
| A、-2012 | B、2012 |
| C、1 | D、-1 |
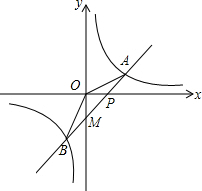 如图,一次函数y=kx-1的图象和反比例函数y=
如图,一次函数y=kx-1的图象和反比例函数y= 如图,数轴上与1、
如图,数轴上与1、